题目内容
已知| |=3,|
|=3,| |=4
|=4
求(1)| |的范围;
|的范围;
(2)若|2 |=12,求|
|=12,求| |的值.
|的值.
解:(1)由题意可得  =3×4×cosθ=12cosθ,其中θ是
=3×4×cosθ=12cosθ,其中θ是 与
与 的夹角,0≤θ≤π.
的夹角,0≤θ≤π.
∴-12≤ ≤12.
≤12.
由于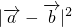 =
= +
+ -2
-2 =25-24cosθ,∴1≤
=25-24cosθ,∴1≤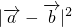 ≤49,∴1≤|
≤49,∴1≤| |≤7,
|≤7,
即| |的范围为[1,7].
|的范围为[1,7].
(2)∵|2 |=12,∴平方可得 4a2-4
|=12,∴平方可得 4a2-4 +
+ =144,∴
=144,∴ =-23.
=-23.
∴ =a2-2
=a2-2 +
+ =9+46+16=71,
=9+46+16=71,
故| |=
|= .
.
分析:(1)由题意可得 =12cosθ,由-12≤
=12cosθ,由-12≤ ≤12,求得
≤12,求得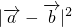 的范围,即可得到|
的范围,即可得到| |的范围.
|的范围.
(2)把|2 |=12,平方可得
|=12,平方可得 =-23,由此求得
=-23,由此求得 的值,即可得到|
的值,即可得到| |的值.
|的值.
点评:本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题.
 =3×4×cosθ=12cosθ,其中θ是
=3×4×cosθ=12cosθ,其中θ是 与
与 的夹角,0≤θ≤π.
的夹角,0≤θ≤π.∴-12≤
 ≤12.
≤12.由于
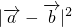 =
= +
+ -2
-2 =25-24cosθ,∴1≤
=25-24cosθ,∴1≤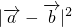 ≤49,∴1≤|
≤49,∴1≤| |≤7,
|≤7,即|
 |的范围为[1,7].
|的范围为[1,7].(2)∵|2
 |=12,∴平方可得 4a2-4
|=12,∴平方可得 4a2-4 +
+ =144,∴
=144,∴ =-23.
=-23.∴
 =a2-2
=a2-2 +
+ =9+46+16=71,
=9+46+16=71,故|
 |=
|= .
.分析:(1)由题意可得
 =12cosθ,由-12≤
=12cosθ,由-12≤ ≤12,求得
≤12,求得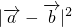 的范围,即可得到|
的范围,即可得到| |的范围.
|的范围.(2)把|2
 |=12,平方可得
|=12,平方可得 =-23,由此求得
=-23,由此求得 的值,即可得到|
的值,即可得到| |的值.
|的值.点评:本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知
<α<π,tanα+cotα=-
,则tanα的值为( )
| 3π |
| 4 |
| 10 |
| 3 |
| A、-3 | ||
B、-
| ||
C、-3或-
| ||
D、-
|