题目内容
已知f(x)=acosx+bsinx+c(x∈R)的图象经过点(0,1),(| π |
| 2 |
| π |
| 2 |
分析:先根据图象经过点(0,1),(
,1),得出a,b,c的关系,将原函数只用一个参数来表示,再结合三角函数的有界性求出函数的最值列不等关系,最后解不等式即可求实数a的取值范围.
| π |
| 2 |
解答:解:由题意,得
(3分)∴f(x)=a(cosx+sinx)+1-a=
asin(x+
)+1-a(5分)
当x∈[0,
]时,x+
∈[
,
],sin(x+
)∈[
,1](8分)
由|f(x)|≤2,得|
a+1-a|≤2(12分)
即-2≤(
-1)a+1≤2?-
≤a≤
解得-3
-3≤a≤
+1(16分)
|
| 2 |
| π |
| 4 |
当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
由|f(x)|≤2,得|
| 2 |
即-2≤(
| 2 |
| 3 | ||
|
| 1 | ||
|
解得-3
| 2 |
| 2 |
点评:本题主要考查了正弦函数的定义域和值域、函数恒成立问题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 ,当
,当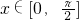 时,恒有|f(x)|≤2,求实数a的取值范围.
时,恒有|f(x)|≤2,求实数a的取值范围. ,则g(x)=asinx+cosx的初相是( )
,则g(x)=asinx+cosx的初相是( )


