题目内容
(本小题12分)
(Ⅰ)从1,3,4,5,7,9这六个数中任取三个数,求这三个数可作为三角形的三条边长的概率.
(Ⅱ)在单位圆的圆周上随机任取三点A、B、C,求![]() 是锐角三角形的概率.
是锐角三角形的概率.
解:(Ⅰ)略解:从1,3,4,5,7,9这六个数中任取三个数的基本事件
的总数为n=20 ----------------2分
记事件A表示这三个数可作为三角形的三条边长,则记事件A发生结果组成集合
为(3,4,5),(3,5,7),(3,7,9),(4,5,7),(4,7,9)(5,7,9)
∴![]() .- ----------------------4分
.- ----------------------4分
(Ⅱ)解法记![]() 的三内角分别为
的三内角分别为![]() ,
,![]() ,事件A表示“
,事件A表示“![]() 是锐角三角形”,则试验的全部结果组成集合
是锐角三角形”,则试验的全部结果组成集合
![]() . ---------------6分 u
. ---------------6分 u
因为![]() 是锐角三角形的条件是
是锐角三角形的条件是
![]() 且
且![]()
所以事件A构成集合
![]() ----------------8分
----------------8分
易知(图略),所求概率为
![]()
 . ----------------12分
. ----------------12分

练习册系列答案
相关题目
 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.
 的圆柱.
的圆柱.
 的方程
的方程
 .
.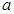 的取值范围.
的取值范围.