题目内容
【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车![]() 辆,混合动力型公交车
辆,混合动力型公交车![]() 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加![]() ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入![]() 辆.设
辆.设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设![]() 、
、![]() 分别为
分别为![]() 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求![]() 、
、![]() ,并求
,并求![]() 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数![]() ;
;
(2)该市计划用![]() 年的时间完成全部更换,求
年的时间完成全部更换,求![]() 的最小值.
的最小值.
【答案】(1)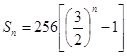 ,
,![]() ,
,![]() ;
;
(2)147.
【解析】
试题(1)设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,通过分析可知数列
年投入的电力型公交车、混合动力型公交车的数量,通过分析可知数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,数列
的等比数列,数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,由等比数列的前
的等差数列,由等比数列的前![]() 项和公式
项和公式![]() ,等差数列的前
,等差数列的前![]() 项和公式
项和公式![]() 即可求出;(2)通过分析
即可求出;(2)通过分析![]() 、
、![]() 是关于
是关于![]() 的单调递增函数,故
的单调递增函数,故![]() 是关于
是关于![]() 的单调递增函数,要求满足
的单调递增函数,要求满足![]() 的最小值应该是
的最小值应该是![]() ,此时应注意实际问题中
,此时应注意实际问题中![]() 取整的问题.
取整的问题.
试题解析:(1)设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,
年投入的电力型公交车、混合动力型公交车的数量,
依题意知,数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列; 1分
的等比数列; 1分
数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列, 2分
的等差数列, 2分
所以数列![]() 的前
的前![]() 项和
项和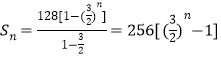 , 4分
, 4分
数列![]() 的前
的前![]() 项和
项和![]() , 6分
, 6分
所以经过![]() 年,该市更换的公交车总数
年,该市更换的公交车总数
![]() ; 7分
; 7分
(2)因为![]() 、
、![]() 是关于
是关于![]() 的单调递增函数, 9分
的单调递增函数, 9分
因此![]() 是关于
是关于![]() 的单调递增函数, 10分
的单调递增函数, 10分
所以满足![]() 的最小值应该是
的最小值应该是![]() , 11分
, 11分
即![]() ,解得
,解得![]()
![]() , 12分
, 12分
又![]() ,所以
,所以![]() 的最小值为147.
的最小值为147.

练习册系列答案
相关题目