题目内容
设F1、F2分别为椭圆C: =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2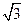 .
.
(1)求椭圆C的焦距;
(2)如果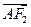 =2
=2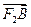 ,求椭圆C的方程.
,求椭圆C的方程.
 =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2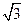 .
.(1)求椭圆C的焦距;
(2)如果
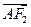 =2
=2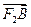 ,求椭圆C的方程.
,求椭圆C的方程.设焦距为2c,则F1(-c,0),F2(c,0)
∵kl=tan60°=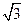
∴l的方程为y=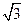 (x-c)
(x-c)
即: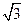 x-y-
x-y-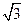 c=0
c=0
∵F1到直线l的距离为2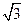
∴c=2
∴椭圆C的焦距为4
(2)设A(x1,y1),B(x2,y2)由题可知y1<0,y2>0
直线l的方程为y=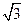 (x-2)
(x-2)
(3a2+b2)y2+4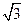 b2y-3b2(a2-4)=0
b2y-3b2(a2-4)=0
∵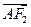 =2
=2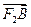 ,∴-y1=2y2,代入①②得
,∴-y1=2y2,代入①②得
得 =
= ⑤
⑤
又a2=b2+4 ⑥
由⑤⑥解得a2=9 b2=5
∴椭圆C的方程为 =1
=1
∵kl=tan60°=
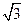
∴l的方程为y=
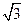 (x-c)
(x-c)即:
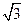 x-y-
x-y-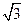 c=0
c=0∵F1到直线l的距离为2
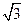
∴c=2
∴椭圆C的焦距为4
(2)设A(x1,y1),B(x2,y2)由题可知y1<0,y2>0
直线l的方程为y=
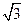 (x-2)
(x-2)(3a2+b2)y2+4
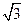 b2y-3b2(a2-4)=0
b2y-3b2(a2-4)=0∵
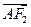 =2
=2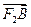 ,∴-y1=2y2,代入①②得
,∴-y1=2y2,代入①②得得
 =
= ⑤
⑤又a2=b2+4 ⑥
由⑤⑥解得a2=9 b2=5
∴椭圆C的方程为
 =1
=1略

练习册系列答案
相关题目
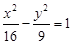 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是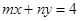 与圆
与圆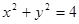 没有交点,则过点
没有交点,则过点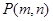 的直线与椭圆
的直线与椭圆 的公共点个数为( )
的公共点个数为( )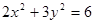 的焦距是( )
的焦距是( )
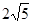

 在
在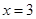 处取得极大值
处取得极大值 .
. 在区间
在区间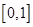 上的最大值;
上的最大值;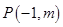 可作曲线
可作曲线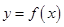 的切线有三条,求实数
的切线有三条,求实数 的取值范围.
的取值范围.
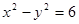 ”是“双曲线离心率
”是“双曲线离心率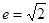 ”的 ( )
”的 ( )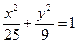 的左、右焦点为
的左、右焦点为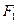 、
、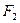 ,
,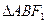 的顶点A、B在椭圆上,且边AB经过右焦点
的顶点A、B在椭圆上,且边AB经过右焦点 标系中,双曲线的中心在原点,焦点在
标系中,双曲线的中心在原点,焦点在 轴上,一条渐近线方程为
轴上,一条渐近线方程为 ,则它的离心率为_____________
,则它的离心率为_____________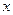 轴上,截直线
轴上,截直线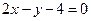 所得弦长为
所得弦长为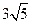 的抛物线方
的抛物线方