题目内容
已知 为等差数列
为等差数列 的前
的前 项和,且
项和,且
 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)求 的通项公式,关键是求等差数列
的通项公式,关键是求等差数列 的首项及公差即
的首项及公差即 ,由已知可知
,由已知可知 ,即
,即 ,解方程组得
,解方程组得 ,有等差数列的通项公式即可写出
,有等差数列的通项公式即可写出 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列 的前
的前 项和
项和 ,首先求出数列
,首先求出数列 的通项公式,由(Ⅰ)可知
的通项公式,由(Ⅰ)可知 ,从而可得
,从而可得 ,分母是等差数列
,分母是等差数列 的连续两项的积,符合利用拆项相消法求和,故
的连续两项的积,符合利用拆项相消法求和,故 ,即可求出.
,即可求出.
试题解析:(Ⅰ)设等差数列 的公差为
的公差为 .因为
.因为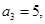
 ,
,
所以 解得
解得 4分
4分
所以 6分
6分
(Ⅱ)

 12分
12分
考点:等差数列的通项公式,数列求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,
, ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 为等差数列
为等差数列 的前
的前 项的和,
项的和, ,
, ,则
,则 的值为( )
的值为( )  C.
C. D.
D. 
 为等差数列
为等差数列 的前
的前 项和,且
项和,且 ,则
,则