题目内容

已知奇函数f(x)=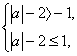

(1)求实数M的值;

(2)若函数f(x)在区间［-1,|a|-2］上单调递增,试确定实数a的取值范围.

解：(1)当x＜0时，-x＞0,?

∴f(-x)=-(-x)2-2x=-x2-2x.                                                                                   ?

又∵f(x)是奇函数，∴f(-x)=-f(x)=-x2-2x.

∴f(x)=x2+2x.∴M=2.                                                                                               ?

(2)由题意，要使函数f(x)在区间［-1,|a|-2］上单调递增，则有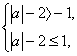

?

解之,得-3≤a＜-1或1＜a≤3.

练习册系列答案
相关题目
已知奇函数f(x)=
-x2+2x(x＞0)
0，(x=0)
x2+mx(x＜0)

（1）求实数m的值，并在给出的直角坐标系中画出y=f（x）的图象．
（2）若函数f（x）在区间[-1，|a|-2]上单调递增，试确定a的取值范围．
已知奇函数f(x)=
ax+b
x2+1
在（-1，1）上是增函数，且f(
1
2
)=
2
5

①确定函数f（x）的解析式．
②解不等式f（t-1）+f（t）＜0．
已知奇函数f(x)=
x2-2x+2  (x＜0)
ax2+bx+c (x＞0)
(a，b，c∈R)，则a+b+c的值是（　　）
已知奇函数f(x)=
-x2+2x   (x＞0)
0
                (x=0)
x2+mx
     (x＜0)
，则m=（　　）
（2008•杭州二模）已知奇函数f(x)=
qx+r
px2+1
有最大值
1
2
，且f(1)＞
2
5
，其中实数x＞0，p、q是正整数．．
（1）求f（x）的解析式；
（2）令an=
1
f(n)
，证明an+1＞an（n是正整数）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网