题目内容
设g(x)=log2x+x,函数 的值域为
的值域为
- A.R
- B.

- C.[0,

- D.

D
分析:由题意,可先化简函数f(x)的解析式,结合g(x)=log2x+x,f(x)的解析式或变为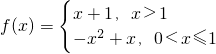 ,分段求出函数的值域,即可先出正确选项
,分段求出函数的值域,即可先出正确选项
解答:由题意g(x)=log2x+x,函数
可得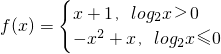 ,
,
即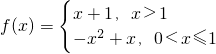
当x>1时,函数的值域是(2,+∞);当0<x≤1时,函数的值域是[0,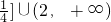
故函数的值域是
故选D
点评:本题考查了解对数函数不等式,求分段函数的值域,一次函数的值域及二次函数的值域,利用解对数不等式得出分段函数的定义域是解题的关键,此也是本题解题的难点,对数运算是高中数学一具重要的运算,对对数的运算性质要熟练掌握灵活运用
分析:由题意,可先化简函数f(x)的解析式,结合g(x)=log2x+x,f(x)的解析式或变为
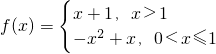 ,分段求出函数的值域,即可先出正确选项
,分段求出函数的值域,即可先出正确选项解答:由题意g(x)=log2x+x,函数

可得
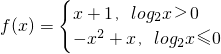 ,
,即
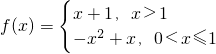
当x>1时,函数的值域是(2,+∞);当0<x≤1时,函数的值域是[0,
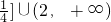
故函数的值域是

故选D
点评:本题考查了解对数函数不等式,求分段函数的值域,一次函数的值域及二次函数的值域,利用解对数不等式得出分段函数的定义域是解题的关键,此也是本题解题的难点,对数运算是高中数学一具重要的运算,对对数的运算性质要熟练掌握灵活运用

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
设函数f(x),g(x)的定义域分别为F、G,且F、G.若对任意的x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是( )
| A、g(x)=2|x| | ||
| B、g(x)=log2|x| | ||
C、g(x)=(
| ||
D、g(x)=log
|