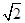题目内容
已知O是 内部一点,
内部一点, 则
则 的面积为( )
的面积为( )
A. | B. | C. | D. |
A
解析试题分析: 是三角形重心,
是三角形重心,
 面积为
面积为 ,所以
,所以 面积为
面积为
考点:向量运算及解三角形
点评:本题中由 得到O为
得到O为 的重心这一结论是求解的关键,而后利用重心的性质(重心到顶点的距离等于到对边中点的距离的2倍)找到两三角形面积间的关系
的重心这一结论是求解的关键,而后利用重心的性质(重心到顶点的距离等于到对边中点的距离的2倍)找到两三角形面积间的关系

练习册系列答案
相关题目
已知 两点,过动点
两点,过动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若 ,当
,当 时,动点
时,动点 的轨迹为( )
的轨迹为( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
已知向量 不共线,
不共线, 如果
如果 //
// 那么 ( )
那么 ( )
A. 且c与d反向 且c与d反向 | B. 且c与d反向 且c与d反向 |
C. 且c与d同向 且c与d同向 | D. 且c与d同向 且c与d同向 |
点O是 ABC所在平面内一定点,动点P满足
ABC所在平面内一定点,动点P满足 ,则动点P的轨迹一定通过三角形ABC的( )
,则动点P的轨迹一定通过三角形ABC的( )
| A.重心 | B.垂心 | C.外心 | D.内心 |
矩阵A ,向量
,向量 ,则A
,则A
 ( )
( )
A. | B. | C. | D. |
已知两点 为坐标原点,点
为坐标原点,点 在第二象限,且
在第二象限,且 ,设
,设 等于 ( )
等于 ( )
A. | B.2 | C.1 | D. |
在 所在的平面内有一点P,如果
所在的平面内有一点P,如果 ,那么
,那么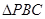 和面积与
和面积与 的面积之比是
的面积之比是
A.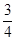 | B. | C. | D. |
 、
、 、
、 满足
满足 ,
, ,
,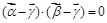 .若对每一确定的
.若对每一确定的 ,
, 的最大值和最小值分别为
的最大值和最小值分别为 、
、 ,则对任意
,则对任意 的最小值是 ( )
的最小值是 ( )