题目内容
一空间几何体的三视图如图所示,求该几何体的体积.
分析:由三视图判断空间几何体是由下圆柱和上四棱锥组成,并根据三视图求出圆柱的半径和高,四棱锥的边长和高,代入对应的体积公式分别求解,最后再和在一起.
解答:解:由三视图得,该空间几何体为一圆柱和一四棱锥组成的,
并且圆柱的底面半径为3,高为6,体积为54π,
四棱锥的底面边长为3
,高为
=4,体积为
•(3
)2•4=24
所以该几何体的体积为54π+24.
并且圆柱的底面半径为3,高为6,体积为54π,
四棱锥的底面边长为3
| 2 |
| 52-32 |
| 1 |
| 3 |
| 2 |
所以该几何体的体积为54π+24.
点评:本题的考点是由三视图求几何体的体积,需要由三视图判断空间几何体的结构特征,并根据三视图求出每个几何体中几何元素的长度,代入对应的体积公式分别求解,考查了空间想象能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
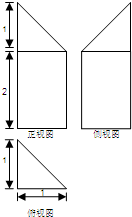
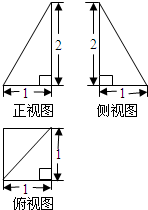
 (2013•成都一模)一空间几何体的三视图如图所示,图中各线段旁的数字表示 该线段的长度,则该几何体的体积为( )
(2013•成都一模)一空间几何体的三视图如图所示,图中各线段旁的数字表示 该线段的长度,则该几何体的体积为( ) (2013•德州一模)一空间几何体的三视图如图所示,该几何体的体积为
(2013•德州一模)一空间几何体的三视图如图所示,该几何体的体积为 (2012•厦门模拟)已知一空间几何体的三视图如图所示,则该几何体中相互垂直的棱共有( )
(2012•厦门模拟)已知一空间几何体的三视图如图所示,则该几何体中相互垂直的棱共有( )