题目内容
如图,
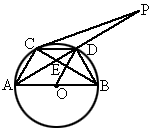
⊙O是以AB为直径的△ABC的外接圆,D是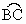 的中点,连结AD并延长与过C点的切线交于P,OD与BC相交于E.
的中点,连结AD并延长与过C点的切线交于P,OD与BC相交于E.
(1)
求证: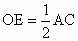 ;
;
(2)
求证: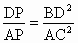 ;
;
(3)
当AC=6,AB=10时,求切线PC的长.
答案:略
解析:
解析:
|
(1) 证明:∵D是 的中点,∴∠CAB=∠DOB,∴AC∥OD. 的中点,∴∠CAB=∠DOB,∴AC∥OD.
又 ∵O为AB中点,OD与CB交于点E,∴ . .
(2) 证明:由弦切角定理知:∠PAC=∠PCD,∠P为公共角,∴△PAC∽△PCD ,∴ ,而 ,而 , ,
∴ 又 ∵DC=BD,∴ . .
(3) 解:由AC=6,AB=10,∴BC=8,BE=4,OE=3,∴DE=OD -OE=5-3=2.∵AC∥OE ,∠ACB=90°,∠OEB=90°,即OD⊥BC.在 Rt△BED中, , ,
∴ ∴ 由 (2)知 , ,
∴  . .
由切割弦定理得  ,∴CP=15. ,∴CP=15. |

练习册系列答案
相关题目




 选修4-1:几何证明选讲
选修4-1:几何证明选讲
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E.
的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E. AC;
AC;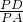 =
= .
. 的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E.
的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E. AC;
AC; =
= .
.
 的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E.
的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E. AC;
AC; =
= .
.
 的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E.
的中点,连接AD并延长,与过C点的切线交于P,OD与BC相交于点E. AC;
AC; =
= .
.