题目内容
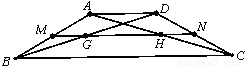
如图,已知ABCD是底角为30°的等腰梯形,AD=2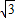 ,BC=4
,BC=4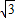 ,取两腰中点M、N分别交对角线BD、AC于G、H,则
,取两腰中点M、N分别交对角线BD、AC于G、H,则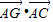 =( )
=( )
A.3
B.4
C.5
D.6
【答案】分析:以BC所在直线为x轴,B为原点建立如图直角坐标系,可得A、B、C、D各点的坐标.利用梯形的中位线定理,结合题中数据算出G(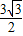 ,
, ),从而得到向量
),从而得到向量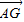 =(
=(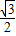 ,-
,- ),再求出向量
),再求出向量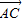 的坐标,利用向量数量积的坐标公式,即可算出
的坐标,利用向量数量积的坐标公式,即可算出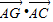 的值.
的值.
解答:解: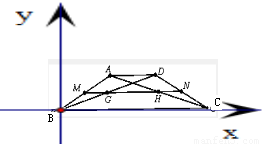 以BC所在直线为x轴,B为原点建立如图直角坐标系
以BC所在直线为x轴,B为原点建立如图直角坐标系
可得A(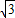 ,1),B(0,0),C(4
,1),B(0,0),C(4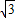 ,0)
,0)
D(3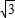 ,1)
,1)
∵MN是梯形ABCD的中位线
∴设G(m, )
)
由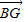 =(m,
=(m, ),
),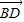 =(3
=(3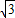 ,1)且
,1)且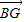 ∥
∥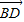
可得m×1=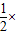 3
3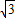 ,解得m=
,解得m=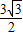 ,G(
,G(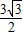 ,
, )
)
由此可得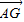 =(
=(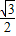 ,-
,- ),
),
∵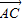 =(3
=(3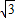 ,-1),∴
,-1),∴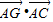 =
=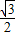 ×3
×3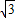 +(-
+(- )•(-1)=5
)•(-1)=5
故选:C
点评:本题给出底角为30度的等腰梯形,求数量积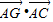 的值.着重考查了向量的坐标运算、向量平行的条件和向量数量积的运算公式等知识,属于中档题.
的值.着重考查了向量的坐标运算、向量平行的条件和向量数量积的运算公式等知识,属于中档题.
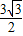 ,
, ),从而得到向量
),从而得到向量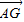 =(
=(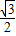 ,-
,- ),再求出向量
),再求出向量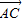 的坐标,利用向量数量积的坐标公式,即可算出
的坐标,利用向量数量积的坐标公式,即可算出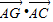 的值.
的值.解答:解:
 以BC所在直线为x轴,B为原点建立如图直角坐标系
以BC所在直线为x轴,B为原点建立如图直角坐标系可得A(
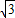 ,1),B(0,0),C(4
,1),B(0,0),C(4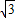 ,0)
,0)D(3
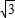 ,1)
,1)∵MN是梯形ABCD的中位线
∴设G(m,
 )
)由
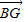 =(m,
=(m, ),
),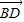 =(3
=(3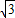 ,1)且
,1)且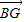 ∥
∥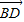
可得m×1=
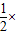 3
3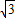 ,解得m=
,解得m=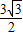 ,G(
,G(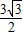 ,
, )
)由此可得
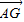 =(
=(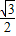 ,-
,- ),
),∵
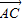 =(3
=(3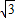 ,-1),∴
,-1),∴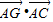 =
=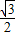 ×3
×3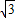 +(-
+(- )•(-1)=5
)•(-1)=5故选:C
点评:本题给出底角为30度的等腰梯形,求数量积
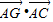 的值.着重考查了向量的坐标运算、向量平行的条件和向量数量积的运算公式等知识,属于中档题.
的值.着重考查了向量的坐标运算、向量平行的条件和向量数量积的运算公式等知识,属于中档题. 
练习册系列答案
相关题目
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1). 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求: 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.