题目内容
已知函数f（x）=x2+bx+1是R上的偶函数，则不等式f（x-1）＜|x|的解集是 ．
分析：根据偶函数的性质可得b=0，从而得到函数f（x）的解析式，不等式即 （x-1）2＜|x|-1，数形结合求得不等式的解集．
解答：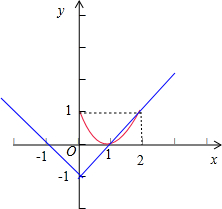
解：∵二次函数f（x）=x2+bx+1是R上的偶函数，故它的对称轴为x=-
=0，即b=0，
∴函数f（x）=x2+1．
∴不等式f（x-1）＜|x|，即（x-1）2+1＜|x|，即（x-1）2＜|x|-1，
故函数y=（x-1）2 的图象（红色部分）在函数 y=|x|-1（蓝色部分）的图象的下方，如图所示：
故不等式f（x-1）＜|x|的解集是 （1，2）．
解：∵二次函数f（x）=x2+bx+1是R上的偶函数，故它的对称轴为x=-| b |
| 2 |
∴函数f（x）=x2+1．
∴不等式f（x-1）＜|x|，即（x-1）2+1＜|x|，即（x-1）2＜|x|-1，
故函数y=（x-1）2 的图象（红色部分）在函数 y=|x|-1（蓝色部分）的图象的下方，如图所示：
故不等式f（x-1）＜|x|的解集是 （1，2）．
点评：本题主要考查函数的奇偶性，绝对值不等式的解法，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|