题目内容
化简:(1)
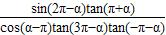 ;
;(2)
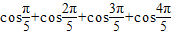 .
.
【答案】分析:(1)原式分子第一项第一个因式利用诱导公式sin(2π-α)=-sinα化简,第二个因式利用tan(π+α)=tanα化简,分母中的第一个因式先利用余弦函数为偶函数进行变形后,再利用诱导公式cos(π-α)=-cosα化简,第二个因式先利用诱导公式tan(2π+α)=tanα化简,再利用正切函数为奇函数变形,最后一项先利用正切函数为奇函数变形后再利用诱导公式tan(π+α)=tanα化简,再利用同角三角函数间的基本关系变形,约分后即可得到最简结果;
(2)将原式第三项中的角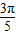 变形为π-
变形为π-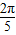 ,
,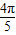 变形为π-
变形为π-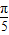 ,然后利用诱导公式cos(π-α)=-cosα化简,合并后即可得到结果.
,然后利用诱导公式cos(π-α)=-cosα化简,合并后即可得到结果.
解答:解:(1)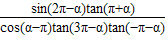
=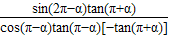
=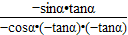
=1;
(2)cos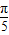 +cos
+cos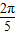 +cos
+cos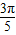 +cos
+cos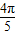
=cos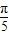 +cos
+cos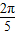 +cos(π-
+cos(π-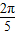 )+cos(π-
)+cos(π-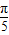 )
)
=cos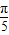 +cos
+cos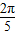 -cos
-cos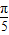 -cos
-cos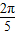
=0.
点评:此题考查了运用诱导公式化简求值,同角三角函数间的基本关系,以及余弦、正切函数的奇偶性,熟练掌握诱导公式是解本题的关键.
(2)将原式第三项中的角
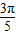 变形为π-
变形为π-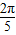 ,
,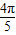 变形为π-
变形为π-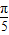 ,然后利用诱导公式cos(π-α)=-cosα化简,合并后即可得到结果.
,然后利用诱导公式cos(π-α)=-cosα化简,合并后即可得到结果.解答:解:(1)
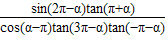
=
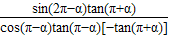
=
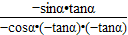
=1;
(2)cos
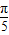 +cos
+cos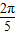 +cos
+cos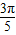 +cos
+cos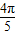
=cos
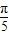 +cos
+cos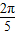 +cos(π-
+cos(π-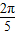 )+cos(π-
)+cos(π-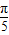 )
)=cos
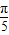 +cos
+cos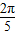 -cos
-cos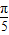 -cos
-cos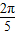
=0.
点评:此题考查了运用诱导公式化简求值,同角三角函数间的基本关系,以及余弦、正切函数的奇偶性,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ;
; 。
。 .(7分)
.(7分) (7分)
(7分)