题目内容
四棱锥S—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=SB=SC=2CD=2,侧面SBC⊥底面ABCD.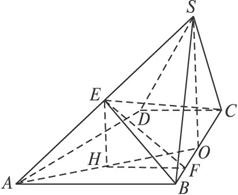
(1)由SA的中点E作底面的垂线EH,试确定垂足H的位置;
(2)求二面角E-BC-A的大小.
解:(1)作SO⊥BC于O,则SO![]() 平面SBC,
平面SBC,

又面SBC⊥底面ABCD,
面SBC∩面ABCD=BC,
∴SO⊥底面ABCD.①
又SO![]() 平面SAO,∴面SAO⊥底面ABCD.
平面SAO,∴面SAO⊥底面ABCD.
作EH⊥AO,∴EH⊥面ABCD,②
即H为垂足,由①②知,EH∥SO.
又E为SA的中点,∴H是AO的中点.
(2)过H作HF⊥BC于F,连EF,由(1)知EH⊥平面ABCD,∴EH⊥BC.
∴BC⊥平面EFH.∴BC⊥EF.
∴∠HFE为面EBC和底面ABCD所成二面角的平面角.
在等边△SBC中,∵SO⊥BC,∴O为BC中点.又BC=2,
∴SO=![]() =
=![]() ,
,
EH=![]() SO=
SO=![]() ,又HF=
,又HF=![]() AB=1,
AB=1,
∴在Rt△EHF中,tan∠HFE=![]() =
=![]() =
=![]() .
.
∴∠HFE=arctan![]() .∴二面角EBCA为arctan
.∴二面角EBCA为arctan![]() .
.

练习册系列答案
相关题目
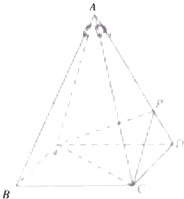 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=