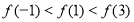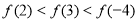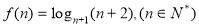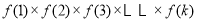题目内容
设不等式
的解集为M，求当x∈M时函数
的最大、最小值.
最小值为
，最大值为8.
【解析】
试题分析：将
看成一个整体，由不等式
得出
，从而得到集合
；将
化简得到一个关于
的二次函数，问题转化成二次函数在某个区间上的最值问题.
试题解析：由
得
， 2分
解得：
， 4分
所以
， 5分
所以
. 6分
=
， 8分
令
，则
. 9分
所以
在
上单调递减， 10分
所以当
时取最小值为
，当
取，. 13分
考点：二次不等式的解法，对数的运算性质，二次函数在某固定区间上的最值，转化与化归思想.
练习册系列答案
相关题目
