题目内容
如图,在正三棱柱ABC—A1B1C1中,AB=AA1,E是棱BB1的中点.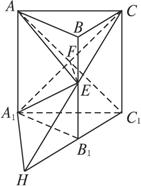
(1)求证:平面A1EC⊥平面AA1C1C;
(2)若我们把平面A1EC与平面A1B1C1所成的锐二面角为60°时的正三棱柱称为“黄金棱柱”,请判断此三棱柱是否为“黄金棱柱”,并说明理由;
(3)设AB=a,求体积![]() .
.
(1)证明:连结A1C与AC1交于点F,连结EF,则由条件可得EC=EA1,则EF⊥A1C.同理,EC1=EA,则EF⊥AC1,

∴EF⊥面AA1C1C.
而EF![]() 面A1EC,∴平面A1EC⊥平面AA1C1C.
面A1EC,∴平面A1EC⊥平面AA1C1C.
〔也可通过如下(2)的辅助线先证明EF∥A1H,而A1H⊥面AA1C1C得到〕
(2)解:延长CE交C1B1的延长线于点H,则有C1B1=B1H=A1B1,则∠HA1C1=90°,且∠CA1H=90°,所以∠CA1C1为平面A1EC与平面A1B1C1所成二面角的平面角.若此正三棱柱为“黄金棱柱”,则∠CA1C1=60°,应有CC1=![]() A1C1,与条件AB=AA1矛盾.
A1C1,与条件AB=AA1矛盾.
所以此三棱柱不能成为“黄金棱柱”.
(也可利用公式cosθ=![]() 得到二面角的平面角来解决)
得到二面角的平面角来解决)
(3)解:![]() =
=![]() C=
C=![]() ·EF·
·EF·![]() AA1·AC=
AA1·AC=![]() ×
×![]() a×a×a=
a×a×a=![]() a3.
a3.
(或通过![]() =
=![]() 来计算).
来计算).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.