题目内容
已知函数f(x)=x3-ax.(a∈R)
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)求证: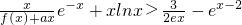 .
.
解(I)f′(x)=3x2-a
当a≤0时,f′(x)≥0恒成立,故函数f(x)在R上单调递增
当a>0时,由由f′(x)≥0可得c×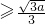 或x
或x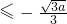
由f′(x)<0可得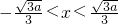
综上可得,a≤0时,f′(x)≥0恒成立,故函数f(x)在R上单调递增
当a>0时,函数f(x)的单调递增区间为( ,+∞),(-∞,-
,+∞),(-∞,- ),单调递减区间(
),单调递减区间(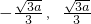 )
)
(II)证明:原不等式可化为xlnx>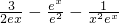
容易得x>0,上式两边同乘以x可得x2lnx
设p(x)=x2lnx,q(x)= -
-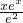 -
-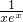 =
=
则由p′(x)=x(2lnx+1)可得x=0(舍)或x=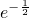
∴ 时,p′(x)<0,x>
时,p′(x)<0,x>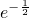 时,p′(x)>0
时,p′(x)>0
∴当x=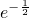 时,函数p(x)取得最小值
时,函数p(x)取得最小值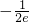
∵q(x)= -
-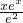 -
-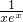 =
=
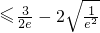 =
=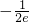
当且仅当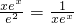 即xex=e时取等号
即xex=e时取等号
令r(x)=xex,可得r(x)在(0,+∞)上单调递增,且r(1)=e
当x=1时,q(x)有最小值q(x)=-
∴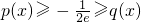
由于上面两个等号不能同时取得,故有p(x)>q(x0,则原不等式成立
分析:(I)先求导,令f′(x)=0,由f′(x)≥0可求函数的递增区间,由f′(x)<0可求函数的单调递减区间
(II)要证明原不等式,可转化为证明x2lnx ,构造函数设p(x)=x2lnx,q(x)=
,构造函数设p(x)=x2lnx,q(x)= -
-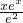 -
-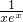 =
= ,利用导数可得当x=
,利用导数可得当x=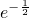 时,函数p(x)取得最小值
时,函数p(x)取得最小值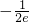 ,利用基本不等式可求q(x)有最小值q(x)=-
,利用基本不等式可求q(x)有最小值q(x)=- ,可证
,可证
点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,而(2)中的证明具有很强的技巧性,综合了导数求解函数的最值,基本不等式求解函数的最值及利用构造函数证明不等式.
当a≤0时,f′(x)≥0恒成立,故函数f(x)在R上单调递增
当a>0时,由由f′(x)≥0可得c×
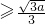 或x
或x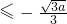
由f′(x)<0可得
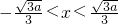
综上可得,a≤0时,f′(x)≥0恒成立,故函数f(x)在R上单调递增
当a>0时,函数f(x)的单调递增区间为(
 ,+∞),(-∞,-
,+∞),(-∞,- ),单调递减区间(
),单调递减区间(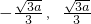 )
)(II)证明:原不等式可化为xlnx>
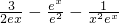
容易得x>0,上式两边同乘以x可得x2lnx

设p(x)=x2lnx,q(x)=
 -
-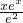 -
-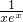 =
=
则由p′(x)=x(2lnx+1)可得x=0(舍)或x=
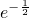
∴
 时,p′(x)<0,x>
时,p′(x)<0,x>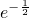 时,p′(x)>0
时,p′(x)>0∴当x=
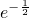 时,函数p(x)取得最小值
时,函数p(x)取得最小值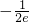
∵q(x)=
 -
-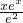 -
-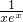 =
=
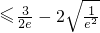 =
=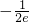
当且仅当
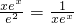 即xex=e时取等号
即xex=e时取等号令r(x)=xex,可得r(x)在(0,+∞)上单调递增,且r(1)=e
当x=1时,q(x)有最小值q(x)=-

∴
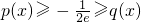
由于上面两个等号不能同时取得,故有p(x)>q(x0,则原不等式成立
分析:(I)先求导,令f′(x)=0,由f′(x)≥0可求函数的递增区间,由f′(x)<0可求函数的单调递减区间
(II)要证明原不等式,可转化为证明x2lnx
 ,构造函数设p(x)=x2lnx,q(x)=
,构造函数设p(x)=x2lnx,q(x)= -
-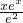 -
-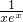 =
= ,利用导数可得当x=
,利用导数可得当x=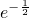 时,函数p(x)取得最小值
时,函数p(x)取得最小值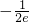 ,利用基本不等式可求q(x)有最小值q(x)=-
,利用基本不等式可求q(x)有最小值q(x)=- ,可证
,可证点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,而(2)中的证明具有很强的技巧性,综合了导数求解函数的最值,基本不等式求解函数的最值及利用构造函数证明不等式.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|