题目内容
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为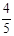 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为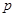 ,
,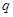 (
(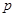 >
>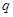 ),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求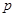 ,
,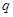 的值;
的值;
(Ⅲ)求数学期望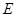 ξ.
ξ.
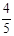 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为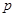 ,
,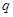 (
(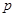 >
>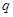 ),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为| ξ | 0 | 1 | 2 | 3 |
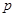 | 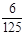 | 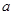 | b | 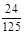 |
(Ⅱ)求
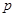 ,
,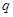 的值;
的值;(Ⅲ)求数学期望
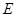 ξ.
ξ.(I)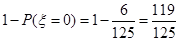 ,(II)
,(II)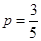 ,
,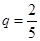 .(III)
.(III)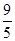
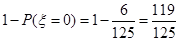 ,(II)
,(II)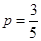 ,
,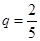 .(III)
.(III)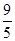
(1)可根据其对立事件来求:其对立事件为:没有一门课程取得优秀成绩.
(2)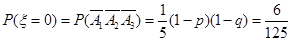
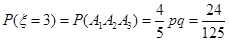
建立关于p、q的方程,解方程组即可求解.
(3)先算出a,b的值,然后利用期望公式求解即可.
事件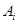 表示“该生第
表示“该生第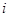 门课程取得优秀成绩”,
门课程取得优秀成绩”,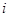 =1,2,3,由题意知
=1,2,3,由题意知
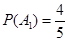 ,
,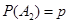 ,
,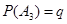
(I)由于事件“该生至少有1门课程取得优秀成绩”与事件“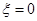 ”是对立的,所以该生至少有1门课程取得优秀成绩的概率是
”是对立的,所以该生至少有1门课程取得优秀成绩的概率是
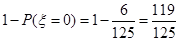 ,
,
(II)由题意知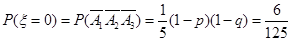
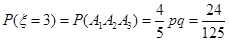
整理得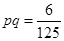 ,
,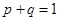 由
由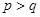 ,可得
,可得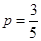 ,
,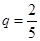 .
.
(III)由题意知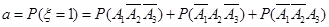
=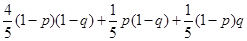
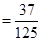
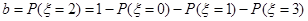 =
=
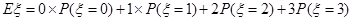 =
=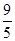
(2)
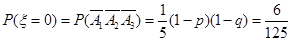
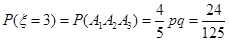
建立关于p、q的方程,解方程组即可求解.
(3)先算出a,b的值,然后利用期望公式求解即可.
事件
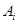 表示“该生第
表示“该生第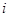 门课程取得优秀成绩”,
门课程取得优秀成绩”,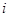 =1,2,3,由题意知
=1,2,3,由题意知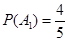 ,
,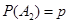 ,
,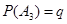
(I)由于事件“该生至少有1门课程取得优秀成绩”与事件“
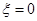 ”是对立的,所以该生至少有1门课程取得优秀成绩的概率是
”是对立的,所以该生至少有1门课程取得优秀成绩的概率是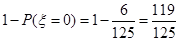 ,
,(II)由题意知
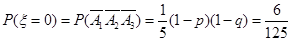
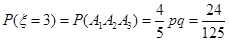
整理得
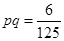 ,
,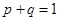 由
由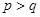 ,可得
,可得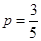 ,
,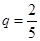 .
.(III)由题意知
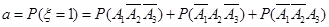
=
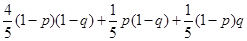
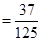
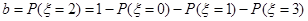 =
=
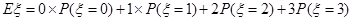 =
=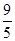

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
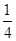 ,不堵车的概率为
,不堵车的概率为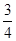 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为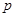 ,不堵车的概率为
,不堵车的概率为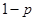 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为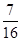 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数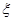 的分布列和数学期望。
的分布列和数学期望。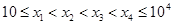 ,
,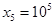 . 随机变量
. 随机变量 取值
取值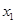 、
、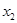 、
、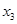 、
、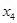 、
、 的概率均为0.2,随机变量
的概率均为0.2,随机变量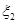 取值
取值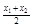 、
、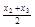 、
、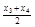 、
、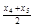 、
、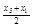 的概率也为0.2.
的概率也为0.2. 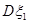 、
、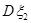 分别为
分别为 为小球编号与盒子编号不一致的数目,则
为小球编号与盒子编号不一致的数目,则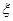 表示取出的竹签的最大号码,则
表示取出的竹签的最大号码,则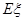 的值是
的值是 .
.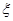 的分布列为下表所示:
的分布列为下表所示: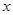
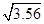 C.3.2 D.
C.3.2 D.