题目内容
（理科）在棱长为1的正方体ABCD-A′B′C′D′中，AC′为对角线，M、N分别为BB′，B′C′中点，P为线段MN中点．
（1）求DP和平面ABCD所成的角的正切；
（2）求DP和AC′所成角．
（1）求DP和平面ABCD所成的角的正切；
（2）求DP和AC′所成角．
（1）过P作PH⊥BC于足H，连DH，
∵面BC′⊥面AC，则PH⊥面ABCD，
∴DP和面ABCD所成角即为∠HDP．
在正方形BCC′B′，M，N分别为BB′，B′C′中点，P为MN中点，
又B′C′=1，则PH=
，BH=
，CH=
，
DH=
=
=
在Rt△PHD中，tan∠HDP=
=
(6分)
（2）建立如图空间直角坐标系
A(0，0，1)，C′(1，1，0)，则
=(1，1，-1)，
D(0，1，1)，P(1，
，
)．
则
=(1，-
，-
)
设
和
夹角为θ
cosθ=
=
θ=arccos
=arccos
(12分)
∵面BC′⊥面AC，则PH⊥面ABCD，
∴DP和面ABCD所成角即为∠HDP．
在正方形BCC′B′，M，N分别为BB′，B′C′中点，P为MN中点，
又B′C′=1，则PH=
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
DH=
| DC2+DH2 |
1+(
|
| 5 |
| 4 |
在Rt△PHD中，tan∠HDP=
| ||
|
| 3 |
| 5 |
（2）建立如图空间直角坐标系
A(0，0，1)，C′(1，1，0)，则
| AC′ |
D(0，1，1)，P(1，
| 1 |
| 4 |
| 1 |
| 4 |
则
| DP |
| 3 |
| 4 |
| 3 |
| 4 |
设
| AC |
| DP |
cosθ=
(1，1，-1)•(1，-
| ||||||||
|
| 4 | ||
|
| 4 | ||
|
2
| ||
| 51 |
练习册系列答案
相关题目
（理科）如图，在棱长为1的正方体A'C中，过BD及B'C'的中点E作截面BEFD交C'D'于F．
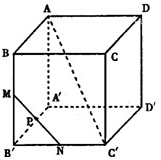（2004•武汉模拟）（理科）在棱长为1的正方体ABCD-A′B′C′D′中，AC′为对角线，M、N分别为BB′，B′C′中点，P为线段MN中点．
如图，在棱长为2的正方体ABCD-A1B1C1D1中，M，N分别是A1A，B1B的中点．