题目内容
下面有四个结论:
①偶函数的图象一定与y轴相交.
②奇函数的图象不一定过原点.
③偶函数若在(0,+∞)上是减函数,则在(-∞,0)上一定是增函数.
④有且只有一个函数既是奇函数又是偶函数.
其中正确结论的个数是
- A.1
- B.2
- C.3
- D.4
B
分析:设函数的定义域为A,根据当0∉A时,函数的图象与y轴无交点,可判断①②,根据偶函数在对称区间上单调性相反,可判断③;根据函数奇偶性的定义及同一函数的判定方法,可判断④
解答:设函数的定义域为A,当0∉A时,函数的图象与y轴无交点,故①错误;②正确;
根据偶函数在对称区间上单调性相反,故③正确;
若函数值恒为0,且定义域A关于原点对称,则该函数既是奇函数又是偶函数.但由于定义域不同函数即为不同函数,故这样的函数有无数个,故④错误
即4个命题中有2个是正确的
故选B
点评:本题考查的知识点是函数的奇偶性与函数的单调性,是函数图象与性质的综合应用,其中易忽视④中定义域不同函数即为不同函数,而错选C
分析:设函数的定义域为A,根据当0∉A时,函数的图象与y轴无交点,可判断①②,根据偶函数在对称区间上单调性相反,可判断③;根据函数奇偶性的定义及同一函数的判定方法,可判断④
解答:设函数的定义域为A,当0∉A时,函数的图象与y轴无交点,故①错误;②正确;
根据偶函数在对称区间上单调性相反,故③正确;
若函数值恒为0,且定义域A关于原点对称,则该函数既是奇函数又是偶函数.但由于定义域不同函数即为不同函数,故这样的函数有无数个,故④错误
即4个命题中有2个是正确的
故选B
点评:本题考查的知识点是函数的奇偶性与函数的单调性,是函数图象与性质的综合应用,其中易忽视④中定义域不同函数即为不同函数,而错选C

练习册系列答案
相关题目
 ,有下面四个结论:①f(x)是偶函数;②当x>2010时,
,有下面四个结论:①f(x)是偶函数;②当x>2010时,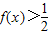 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ;④f(x)的最小值是
;④f(x)的最小值是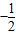 .其中正确结论的序号是 .
.其中正确结论的序号是 .