题目内容
（本题满分16分）
数列
是首项
的等比数列，且
，
，
成等差数列，
（Ⅰ）求数列的通项公式；
（Ⅱ）若
，设
为数列
的前
项和，若≤
对一切
恒成立，求实数
的最小值.
解：（1）当
时，
,不成等差数列。…………2分
当
时，
，
（若没用求和公式则无需上面分类讨论）
∴
， ∴
，∴
…………6分
∴
…………7分
（2）
…………9分
…………12分
≤
，∴
≤
…………14分
∴
≥
又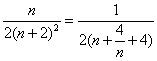
≤
，（也可以利用函数的单调性解答）
∴的最小值为
…………16分
练习册系列答案
发散思维新课堂系列答案
相关题目
（
，
、
是常数，且
），对定义域内任意
（
且
），恒有
成立．
的解析式，并写出函数的定义域；
．
的前
项和为
，且
．数列
中，
，
．（1）求数列
使数列
是等比数列，求数列
；②
．
在
上的单调性；
，使
，则称
的不动点，现已知该函数有且仅有一个不动点，求
的值；
在