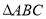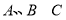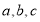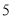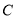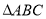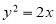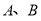题目内容
抛物线 ,其准线方程为
,其准线方程为 ,过准线与
,过准线与 轴的交点
轴的交点 做直线
做直线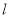 交抛物线于
交抛物线于 两点.
两点.
(1)若点 为
为 中点,求直线
中点,求直线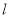 的方程;
的方程;
(2)设抛物线的焦点为 ,当
,当 时,求
时,求 的面积.
的面积.
(1) 或
或 ;(2)4.
;(2)4.
【解析】
试题分析:(1)首先根据准线方程求得抛物线的标准方程,然后设直线直线l的方程 ,并与抛物线方程联立消去x得到关于y的二次方程,再利用韦达定理与中点坐标公式可求得m的值,进而得到直线l的方程;(2)根据条件中的垂直关系,利用A、B、F三点的坐标表示出向量
,并与抛物线方程联立消去x得到关于y的二次方程,再利用韦达定理与中点坐标公式可求得m的值,进而得到直线l的方程;(2)根据条件中的垂直关系,利用A、B、F三点的坐标表示出向量 与
与 ,然后利用向量垂直的条件可得
,然后利用向量垂直的条件可得 的值,进而可求得
的值,进而可求得 的面积.
的面积.
试题解析:(1)∵抛物线的准线方程为 ,∴
,∴
∴抛物线的方程为 ,
,
显然,直线 与坐标轴不平行
与坐标轴不平行
∴设直线 的方程为
的方程为 ,
, ,
,
联立直线与抛物线的方程 ,得
,得 ,
,
 ,解得
,解得 或
或 .
.
∵点 为
为 中点,∴
中点,∴ ,即
,即
∴ 解得
解得 ,
,
 ,∴
,∴ 或
或
∴ ,
,
直线方程为 或
或 .
.
(2)焦点 ,
,
∵


∴ ,
,

 .
.
考点:1、直线方程;2、抛物线方程;3、直线与抛物线的位置关系;4、平面向量垂直的充要条件的应用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目