题目内容
如图,PA⊥平面ABC,满足PA=AB=AC=BC=a,则平面PBC与平面ABC所成的二面角的正切值为___________.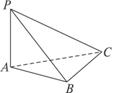
答案: ![]()
解析:取BC的中点E,连结AE、PE,由AC=AB可知AE⊥BC,由于PA⊥平面ABC,故根据三垂线定理知PE⊥BC,故∠PEA即为所求,在Rt△PAE中,tan∠PAE= .
.

练习册系列答案
相关题目
题目内容
如图,PA⊥平面ABC,满足PA=AB=AC=BC=a,则平面PBC与平面ABC所成的二面角的正切值为___________.
答案: ![]()
解析:取BC的中点E,连结AE、PE,由AC=AB可知AE⊥BC,由于PA⊥平面ABC,故根据三垂线定理知PE⊥BC,故∠PEA即为所求,在Rt△PAE中,tan∠PAE= .
.
