题目内容
计算:
(1)(lg5)2+lg2·lg50;(2)(log2125+log425+log85)·(log1258+log254+log52).
答案:
解析:
提示:
解析:
解:(1)原式=(lg5)2+lg2(1+lg5)=lg2+lg5(lg5+lg2)=lg2+lg5·lg10=lg2+lg5=1.
(2)原式=(3log25+log25+![]() log25)(log52+log52+log52)=
log25)(log52+log52+log52)=![]() log25·3log52=13log25·log52=13.
log25·3log52=13log25·log52=13.
提示:
思路分析:本题考查对数的运算性质.(1)充分利用lg2+lg5=1求解;(2)利用换底公式化为底数相同的对数来解决.
绿色通道:化简、计算含有具体实数的对数式值时,要灵活运用对数的相关公式求解,特别是换底公式和一些常见的结论lg2+lg5=1,logab·logba=1等.

练习册系列答案
相关题目
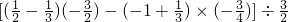 .
. .
.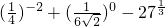 ;
; +log2(log216)+ln(e
+log2(log216)+ln(e )-
)-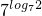 .
.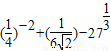 ;
;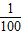 +log2(log216)+ln(e
+log2(log216)+ln(e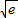 )-
)-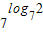 .
.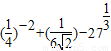 ;
;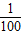 +log2(log216)+ln(e
+log2(log216)+ln(e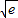 )-
)- .
.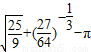
 -lg
-lg +lg12.5-log89•log98.
+lg12.5-log89•log98.