题目内容
圆 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.相交 | D.内含 |
C
解析试题分析:两圆的位置关系判定方法是利用圆心距与两圆半径和差间的关系来判定:圆 、圆
、圆 的半径分别为
的半径分别为 ,则
,则
 两圆外离,
两圆外离,
 两圆外切,
两圆外切,
 两圆相交,
两圆相交,
 两圆内切,
两圆内切,
 两圆内含.
两圆内含.
考点:两圆的位置关系.

练习册系列答案
相关题目
点 是直线
是直线 上动点,
上动点, 是圆
是圆 :
: 的两条切线,
的两条切线, 是切点,若四边形
是切点,若四边形 的最小面积是
的最小面积是 ,则
,则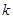 的值为( )
的值为( )
A. | B. | C. | D. |
若直线 被圆
被圆 截得的弦最短,则直线
截得的弦最短,则直线 的方程是( )
的方程是( )
A. | B. | C. | D. |
设椭圆 +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
| A.必在圆x2+y2=2内 | B.必在圆x2+y2=2上 |
| C.必在圆x2+y2=2外 | D.以上三种情形都有可能 |
设椭圆 的离心率为
的离心率为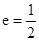 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点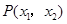 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
圆 的圆心坐标和半径分别是( )
的圆心坐标和半径分别是( )
| A.(0,2) 2 | B.(2,0) 4 |
| C.(-2,0) 2 | D.(2,0) 2 |
过点 作圆
作圆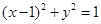 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )
A. | B. | C. | D.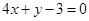 |
直线 与圆
与圆 相切,则实数
相切,则实数 等于( )
等于( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
A. | B. | C. | D. |