题目内容
(文)设a,b,x,y,是正数,且a2+b2=10,x2+y2=40,ax+by=20,则
=( )
| a+b |
| x+y |
分析:通过三角函数的代换即可得出角度之间的关系,进而可求出答案.
解答:解:由a,b,x,y,是正数,且a2+b2=10,x2+y2=40,可设
,
,且α,β∈(0,
).
又∵ax+by=20,∴20cosαcosβ+20sinαsinβ=20,∴cos(α-β)=1,∴α=β+2kπ(k∈Z).
∴
=
=
×
=
×
=
×
=
.
故选C.
|
|
| π |
| 2 |
又∵ax+by=20,∴20cosαcosβ+20sinαsinβ=20,∴cos(α-β)=1,∴α=β+2kπ(k∈Z).
∴
| a+b |
| x+y |
| ||
2
|
| 1 |
| 2 |
| cosα+sinα |
| cosβ+sinβ |
| 1 |
| 2 |
| cos(β+2kπ)+sin(β+2kπ) |
| cosβ+sinβ |
| 1 |
| 2 |
| cosβ+sinβ |
| cosβ+sinβ |
| 1 |
| 2 |
故选C.
点评:恰当利用三角函数的代换是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
=



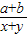 =( )
=( )


