题目内容

已知cosθ1＞sinθ2＞0,cosθ2＞sinθ1＞0.求证:对于任意的整数k总存在相应的θ1、θ2,使得|θ1+?θ2-2kπ|＜.

证明: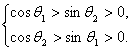

将两式相乘可得cosθ1cosθ2＞sinθ1sinθ2＞0,

∴cosθ1cosθ2-sinθ1sinθ2＞0,

即cos(θ1+θ2)＞0.

∴2kπ-＜θ1+θ2＜2kπ+,

即|θ1+θ2-2kπ|＜(k∈Z).

练习册系列答案
相关题目
已知cosβ=a，sinα=4sin（α+β），则tan（α+β）的值是（　　）
A、
1-a2
a-4
B、-
1-a2
a-4
C、±
a-4
1-a2
D、±
1-a2
a-4
（1）求值sin
π
2
-cos
13π
6
-sin(-
5π
3
)
（2）已知cosα=-
4
5
，sinα-
tan2a+1
的值．
已知
a
=(1，sinθ)，
b
=(1，cosθ)，θ∈R；
（1）若
a
+
b
=(2，0)，求sin2θ+2sinθcosθ的值；
（2）若
a
-
b
=(0，
1
5
)，θ∈（π，2π），求sinθ+cosθ的值．
已知cosβ=-
1
3
，sin（α+β）=
7
9
，α∈（0，
π
2
），β∈（
π
2
，π）．
（1）求cos2β的值；
（2）求sinα的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网