题目内容
函数f(x)的定义域为{x∈R|x≠1},对定义域中的任意的x,都有f(2-x)=-f(x),且当x<1时,f(x)=2x2-x+1,那么当x>1时,f(x)的递减区间是
- A.
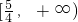
- B.
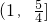
- C.

- D.
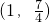
C
分析:先确定当x>1时,f(x)的解析式,再配方,即可求得函数的递减区间.
解答:设x>1,则2-x<1
∵当x<1时,f(x)=2x2-x+1,
∴f(2-x)=2(2-x)2-(2-x)+1,
∵f(2-x)=-f(x),
∴f(x)=-2(2-x)2+(2-x)-1=-2(x- )2-
)2- ,
,
∴当x>1时,f(x)的递减区间是
故选C.
点评:本题考查函数解析式的确定,考查函数的单调性,正确确定函数的解析式是关键.
分析:先确定当x>1时,f(x)的解析式,再配方,即可求得函数的递减区间.
解答:设x>1,则2-x<1
∵当x<1时,f(x)=2x2-x+1,
∴f(2-x)=2(2-x)2-(2-x)+1,
∵f(2-x)=-f(x),
∴f(x)=-2(2-x)2+(2-x)-1=-2(x-
 )2-
)2- ,
,∴当x>1时,f(x)的递减区间是

故选C.
点评:本题考查函数解析式的确定,考查函数的单调性,正确确定函数的解析式是关键.

练习册系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |