题目内容
若sin(π-α)-cos(-α)= ,则sin3(π+α)-cos3(π-α)的值是
,则sin3(π+α)-cos3(π-α)的值是
- A.-

- B.
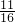
- C.-
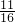
- D.-

C
分析:先根据已知条件求出sinα-cosα= 以及sinα•cosα=
以及sinα•cosα= ;再对所求问题整理后结合三次展开式即可求出结论.
;再对所求问题整理后结合三次展开式即可求出结论.
解答:∵sin(π-α)-cos(-α)= ,
,
∴sinα-cosα= .
.
两边平方得:1-2sinαcosα= ,
,
所以sinα•cosα= .
.
又因为:sin3(π+α)-cos3(π-α)=-sin3α+cos3α
=-(sinα-cosα)(sin2α+sinαcosα+cos2α)
=- ×(1+
×(1+ )=-
)=-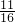 .
.
故选:C.
点评:本题主要考查诱导公式以及三次展开式的应用.解决此类问题的关键在于对公式的熟练掌握以及应用.
分析:先根据已知条件求出sinα-cosα=
 以及sinα•cosα=
以及sinα•cosα= ;再对所求问题整理后结合三次展开式即可求出结论.
;再对所求问题整理后结合三次展开式即可求出结论.解答:∵sin(π-α)-cos(-α)=
 ,
,∴sinα-cosα=
 .
.两边平方得:1-2sinαcosα=
 ,
,所以sinα•cosα=
 .
.又因为:sin3(π+α)-cos3(π-α)=-sin3α+cos3α
=-(sinα-cosα)(sin2α+sinαcosα+cos2α)
=-
 ×(1+
×(1+ )=-
)=-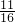 .
.故选:C.
点评:本题主要考查诱导公式以及三次展开式的应用.解决此类问题的关键在于对公式的熟练掌握以及应用.

练习册系列答案
相关题目