题目内容
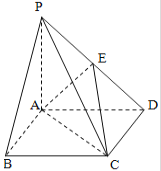
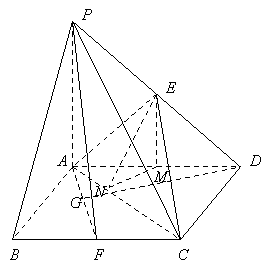
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得点
,使得点![]() 到平
到平
面![]() 的距离为
的距离为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;
的位置;
若不存在,请说明理由.
【答案】解法一:
(Ⅰ)证明:∵底面![]() 为正方形,
为正方形,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() . 2分
. 2分
同理![]() , 4分
, 4分
∴![]() 平面
平面![]() .
.
5分
(Ⅱ)解:设![]() 为
为![]() 中点,连结
中点,连结![]() ,
,
又![]() 为
为![]() 中点,
中点,
可得![]() ,从而
,从而![]() 底面
底面![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
由三垂线定理有![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角. 7分
的平面角. 7分
在![]() 中,可求得
中,可求得![]()
∴![]() . 9分
. 9分
∴ 二面角![]() 的大小为
的大小为![]() . 10分
. 10分
(Ⅲ)解:由![]() 为
为![]() 中点可知,
中点可知,
要使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
即要点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,
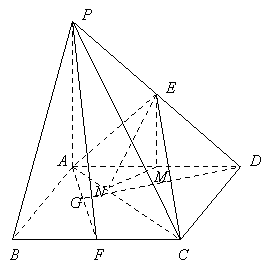
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
∴![]() ,
,
∴![]() . 12分
. 12分
设![]() ,
,
由![]() 与
与![]() 相似可得
相似可得
![]() ,
,
∴![]() ,即
,即![]() .
.
∴在线段![]() 上存在点
上存在点![]() ,且
,且![]() 为
为![]() 中点,使得点
中点,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
14分
解法二:
(Ⅰ)证明:同解法一.
(Ⅱ)解:建立如图的空间直角坐标系![]() , 6分
, 6分
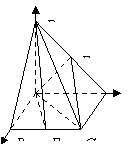
则![]()
![]()
![]() .
.
设![]()
![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则![]()
![]() ,
,![]()
![]() .
.
又![]()
![]()
![]()
令![]() 则
则![]()
得![]()
![]() . 8分
. 8分
又![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
9分
设二面角![]() 的大小为
的大小为 ![]() ,
,
则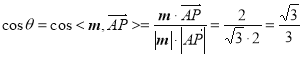 .
.
∴ 二面角![]() 的大小为
的大小为![]() . 10分
. 10分
(Ⅲ)解:设![]()
![]()
![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则![]()
![]() ,
,![]()
![]() .
.
又![]() ,
,![]()
![]()
令![]() 则
则![]()
得![]()
![]() . 12分
. 12分
又![]()
∴点![]() 到平面
到平面![]() 的距离
的距离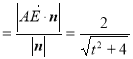 ,
,
∴![]()
![]() ,
,
解得![]() ,即
,即 ![]() .
.
∴在线段![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,且
,且![]() 为
为![]() 中点.14分
中点.14分
【解析】
试题分析:解法一:
(Ⅰ)证明:∵底面![]() 为正方形,
为正方形,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() . 2分
. 2分
同理![]() , 4分
, 4分
∴![]() 平面
平面![]() .
.
5分
(Ⅱ)解:设![]() 为
为![]() 中点,连结
中点,连结![]() ,
,
又![]() 为
为![]() 中点,
中点,
可得![]() ,从而
,从而![]() 底面
底面![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
由三垂线定理有![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角. 7分
的平面角. 7分
在![]() 中,可求得
中,可求得![]()
∴![]() . 9分
. 9分
∴ 二面角![]() 的大小为
的大小为![]() . 10分
. 10分
(Ⅲ)解:由![]() 为
为![]() 中点可知,
中点可知,
要使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
即要点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
∴![]() ,
,
∴![]() . 12分
. 12分
设![]() ,
,
由![]() 与
与![]() 相似可得
相似可得
![]() ,
,
∴![]() ,即
,即![]() .
.
∴在线段![]() 上存在点
上存在点![]() ,且
,且![]() 为
为![]() 中点,使得点
中点,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() .14分
.14分
解法二:
(Ⅰ)证明:同解法一.
(Ⅱ)解:建立如图的空间直角坐标系![]() , 6分
, 6分

则![]()
![]()
![]() .
.
设![]()
![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则![]()
![]() ,
,![]()
![]() .
.
又![]()
![]()
![]()
令![]() 则
则![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案