题目内容
设数列 的前
的前 项和为
项和为 ,
, 
(1)若 ,求
,求 ;
;
(2)若 ,求
,求 的前6项和
的前6项和 ;
;
(3)若 ,证明
,证明 是等差数列.
是等差数列.
(1) ;(2)
;(2) ;(3)只需证
;(3)只需证 。
。
解析试题分析:(1)




即 ,
, 是公比为2的等比数列,且
是公比为2的等比数列,且 3分
3分 即
即


 5分
5分
(2) ,
, 

 是首项为
是首项为 ,公比为
,公比为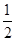 的等比数列 8分
的等比数列 8分 10分
10分
(3) 

即
 是等差数列 14分
是等差数列 14分
考点:等差数列的性质;数列通项公式的求法;数列前n项和的求法;等比数列的前n项和公式。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论 的情况。
的情况。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
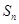 为数列
为数列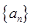 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有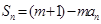 (
(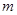 为正常数).
为正常数).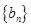 满足
满足 求数列
求数列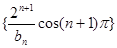 的前
的前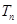 .
. ,
,
 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, .
. 满足
满足 ,求数列
,求数列 项和
项和 .
. }满足
}满足 =3,
=3,  =
=  。设
。设 ,证明数列{
,证明数列{ }是等差数列并求通项
}是等差数列并求通项 .
. 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列 ,求证:
,求证: 轴的距离构成数列
轴的距离构成数列 ,求
,求 的前
的前 项和
项和 .
. 是一个等差数列,
是一个等差数列,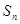 是其前
是其前 项和,且
项和,且 ,
, .
.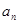 ;
; 的前10项的和
的前10项的和
 是等差数列,其中
是等差数列,其中 [来]
[来] 值。]
值。]