题目内容
【题目】已知函数f(x)=aln x+![]() (a∈R).
(a∈R).
(1)当a=1时,求f(x)在x∈[1,+∞)内的最小值;
(2)若f(x)存在单调递减区间,求a的取值范围;
(3)求证ln(n+1)>![]() (n∈N*).
(n∈N*).
【答案】(1)最小值为f(1)=1.(2)a<![]() .(3)见解析
.(3)见解析
【解析】
试题(1)可先求f′(x),从而判断f(x)在x∈[1,+∞)上的单调性,利用其单调性求f(x)在x∈[1,+∞)最小值;
(2)求h′(x),可得![]() ,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:
,若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:![]() 有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;
有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;
(3)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1![]() ,即
,即![]() 时命题成立;设当n=k时,命题成立,即
时命题成立;设当n=k时,命题成立,即![]() 成立,再去证明n=k+1时,
成立,再去证明n=k+1时,![]() 成立即可(需用好归纳假设).
成立即可(需用好归纳假设).
试题解析:(1)![]() ,定义域为
,定义域为![]() .
.
![]()
![]() 在
在![]() 上是增函数.
上是增函数.
![]() .
.
(2)因为![]()
因为若![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() 有正数解.
有正数解.
即![]() 有
有![]() 的解
的解
当![]() 时,明显成立 .
时,明显成立 .
②当![]() 时,
时,![]() 开口向下的抛物线,
开口向下的抛物线,![]() 总有
总有![]() 的解;
的解;
③当![]() 时,
时,![]() 开口向上的抛物线,
开口向上的抛物线,
即方程![]() 有正根.
有正根.
因为![]() ,
,
所以方程![]() 有两正根.
有两正根.
当![]() 时,
时,![]() ;
;
![]() ,解得
,解得![]() .
.
综合①②③知:![]() .
.
或:
![]() 有
有![]() 的解
的解
即![]() 有
有![]() 的解,
的解,
即![]() 有
有![]() 的解,
的解,
![]() 的最大值
的最大值![]() ,
,![]()
(3)(法一)根据(Ⅰ)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,![]() .
.
![]() ,
,
![]() .
.
(法二)当![]() 时,
时,![]() .
.
![]() ,
,![]() ,即
,即![]() 时命题成立.
时命题成立.
设当![]() 时,命题成立,即
时,命题成立,即![]() .
.
![]() 时,
时,![]()
![]() .
.
根据(Ⅰ)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
则有![]() ,即
,即![]() 时命题也成立.
时命题也成立.
因此,由数学归纳法可知不等式成立.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 地区2019年足球特色学校的个数(精确到个)
地区2019年足球特色学校的个数(精确到个)
参考公式: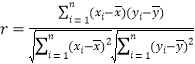 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.