题目内容
已知函数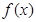 在R上是单调函数,且满足对任意
在R上是单调函数,且满足对任意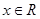 ,都有
,都有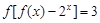 ,若则
,若则 的值是( )
的值是( )
| A.3 | B.7 | C.9 | D.12 |
C
解析试题分析:根据题意,因为函数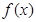 在R上是单调函数,那么对于不同的x的取值,对应的y值不同,由于对于任意的
在R上是单调函数,那么对于不同的x的取值,对应的y值不同,由于对于任意的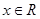 ,都有
,都有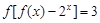 ,则可知
,则可知 是个常数,那么则设
是个常数,那么则设 ,所以可知有
,所以可知有 ,故选C.
,故选C.
考点:本试题考查了函数的单调性和函数的解析式的运用。
点评:解决该试题的关键是利用函数单调性和函数值为常数,说明了函数f(x)的表达式的特点,然后接合已知条件可知,参数的值,进而求解函数值。体现了特殊化思想的运用。属于中档题。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
定义在 上的函数
上的函数 满足
满足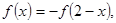 且当
且当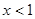 时
时 递增, 若
递增, 若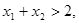
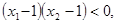 则
则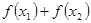 的值是 ( )
的值是 ( )
| A.恒为正数 | B.恒为负数 | C.等于0 | D.正、负都有可能 |
设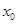 是函数
是函数 的零点,若有
的零点,若有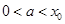 ,则
,则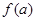 的值满足
的值满足
A.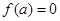 | B. | C. | D.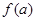 的符号不确定 的符号不确定 |
下列各组函数是同一函数的是( )
①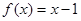 与
与 ; ②
; ②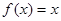 与
与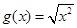 ;
;
③ 与
与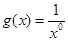 ; ④
; ④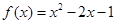 与
与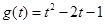 。
。
| A.①② | B.①③ | C.③④ | D.①④ |
函数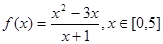 的值域是( )
的值域是( )
| A.[0,2] | B.[0,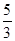 ] ] | C.[-1,2] | D.[-1,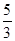 ] ] |
下列函数中,值域为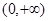 的是( )
的是( )
A.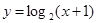 | B.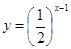 | C.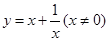 | D.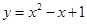 |
设 用二分法求方程
用二分法求方程 在区间(1,2)上近似解的过程中,计算得到
在区间(1,2)上近似解的过程中,计算得到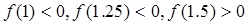 ,则方程的根落在区( )
,则方程的根落在区( )
| A.(1,1.25) | B.(1.25,1.5) | C.(1.5, 1.75) | D.(1.75,2) |
已知定义在R上的奇函数 和偶函数
和偶函数 满足
满足
 ,若
,若 ,则
,则
A. | B. | C. | D.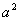 |
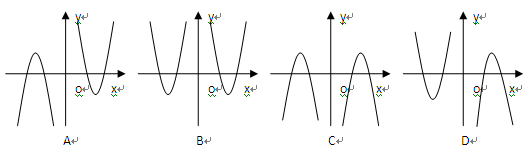
 则
则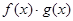 的图象为( )
的图象为( )