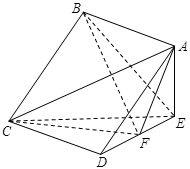题目内容
如图,三棱柱 的侧棱
的侧棱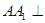 平面
平面 ,
, 为等边三角形,侧面
为等边三角形,侧面 是正方形,
是正方形, 是
是 的中点,
的中点, 是棱
是棱 上的点.
上的点.
(1)若 是棱
是棱 中点时,求证:
中点时,求证: 平面
平面 ;
;
(2)当 时,求正方形
时,求正方形 的边长.
的边长.
详见解析
解析试题分析:(1) 取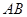 的中点为
的中点为 ,连接
,连接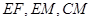 ,由题设可知,
,由题设可知, 为
为 的中点,易证
的中点,易证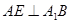 ,可证四边形
,可证四边形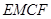 是平行四边形,所以
是平行四边形,所以 ,依据正三棱柱的条件,易证
,依据正三棱柱的条件,易证 ,
,
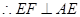 ,这样
,这样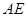 和平面
和平面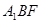 内的两条相交直线垂直,所以
内的两条相交直线垂直,所以 平面
平面 ;
;
(2)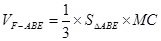 ,只要设正方形的边长为
,只要设正方形的边长为 ,那么根据第一问的结论,用
,那么根据第一问的结论,用 可以表示
可以表示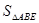 与高
与高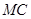 ,根据体积为
,根据体积为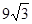 ,即可求出
,即可求出 .
.
(1)取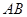 的中点为
的中点为 ,连接
,连接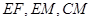 ,
,
 是
是 的中点,
的中点,  是棱
是棱 中点,
中点, ∥
∥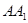 ,
,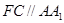 ,
,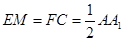 ,
,
则四边形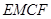 是平行四边形,
是平行四边形, ,
,
又因为 为正三角形,侧面
为正三角形,侧面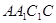 是正方形,
是正方形,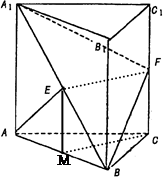
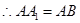 ,所以
,所以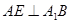 ,
,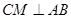 ,
,
因为侧棱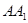 ⊥平面
⊥平面 ,所以
,所以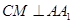 ,
, ,
, ,所以
,所以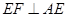 ,
,
又因为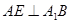 ,
,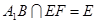 ,所以
,所以 平面
平面 . 6分
. 6分
(2)设正方形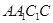 的边长为
的边长为
由于E是 的中点,△EAB的面积为定值。
的中点,△EAB的面积为定值。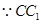 ∥平面
∥平面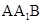 ,
, 点F到平面
点F到平面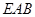 的距离为定值
的距离为定值
即为点C到平面平面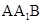 的距离
的距离
又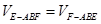 ,且
,且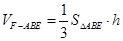 =
=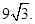
即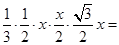
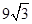 ,
,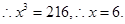 所以正方形的边长为6. 12分
所以正方形的边长为6. 12分
考点:1.线面垂直的判定定理2.面面垂直的判定定理;3.体积公式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.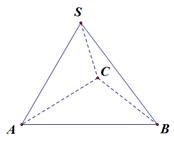
 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,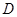 ,
,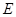 分别是
分别是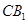 的中点,
的中点,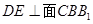 .
. ;
; ;
;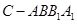 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.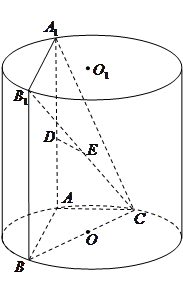

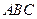 —
—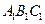 中,侧棱垂直底面,
中,侧棱垂直底面, ,
,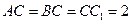 。
。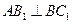 ;
; —
—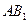 —
—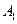 的大小。
的大小。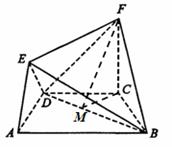

 中,
中, ,
, ,点
,点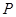 为
为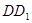 的中点。
的中点。
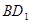 ∥平面
∥平面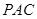 ;
;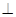 平面
平面 ;
; 中,底面
中,底面 为正方形,
为正方形, 平面
平面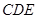 ,已知
,已知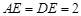 ,
, 为线段
为线段 的中点.
的中点.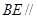 平面
平面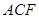 ;
;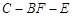 的平面角的余弦值.
的平面角的余弦值.