题目内容
已知f(x)=cos(x+ )-ksinx,且f(
)-ksinx,且f( )=
)= .
.
(1)求实数k的值;
(2)求函数f(x)的最大值及取得最大值时的x值.
解:(1)由已知f(x)=cos(x+ )-ksinx,且f(
)-ksinx,且f( )=
)= ,
,
所以f( )=cos(
)=cos( +
+ )-ksin
)-ksin =
= ,即-
,即- k=
k= ,
,
解得k= (4分)
(4分)
(2)由(1)可知f(x)=cos(x+ )+
)+ sinx (5分)
sinx (5分)
=cosxcos -sinxsin
-sinxsin +
+ sinx (6分)
sinx (6分)
= (7分)
(7分)
=sin(x+ ) (9分)
) (9分)
∴当x+ =2kπ+
=2kπ+ ,k∈Z,即x=2kπ
,k∈Z,即x=2kπ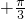 ,k∈Z时 (11分)
,k∈Z时 (11分)
函数f(x)的最大值为1. (12分)
分析:(1)直接利用函数的表达式与f( )=
)= ,求出k即可.
,求出k即可.
(2)求出函数的表达式,通过两角和的正弦函数与余弦函数,化简函数为 一个角的一个三角函数的形式,通过正弦函数的最大值求出函数的最大值以及x的值即可.
点评:本题考查三角函数的值的求法,三角函数的化简求值,函数的基本性质的应用,考查计算能力.
 )-ksinx,且f(
)-ksinx,且f( )=
)= ,
,所以f(
 )=cos(
)=cos( +
+ )-ksin
)-ksin =
= ,即-
,即- k=
k= ,
,解得k=
 (4分)
(4分)(2)由(1)可知f(x)=cos(x+
 )+
)+ sinx (5分)
sinx (5分)=cosxcos
 -sinxsin
-sinxsin +
+ sinx (6分)
sinx (6分)=
 (7分)
(7分)=sin(x+
 ) (9分)
) (9分)∴当x+
 =2kπ+
=2kπ+ ,k∈Z,即x=2kπ
,k∈Z,即x=2kπ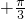 ,k∈Z时 (11分)
,k∈Z时 (11分)函数f(x)的最大值为1. (12分)
分析:(1)直接利用函数的表达式与f(
 )=
)= ,求出k即可.
,求出k即可.(2)求出函数的表达式,通过两角和的正弦函数与余弦函数,化简函数为 一个角的一个三角函数的形式,通过正弦函数的最大值求出函数的最大值以及x的值即可.
点评:本题考查三角函数的值的求法,三角函数的化简求值,函数的基本性质的应用,考查计算能力.

练习册系列答案
相关题目