题目内容
在平面直角坐标系中,直线l的参数方程是 (t是参数,0≤α<π),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ-
(t是参数,0≤α<π),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ- ),直线l与曲线C相交于A、B两点.
),直线l与曲线C相交于A、B两点.
(I)求曲线C的直角坐标方程,并指出它是什么曲线;
(II)若|AB|≥ ,求α的取值范围.
,求α的取值范围.
解:(Ⅰ)曲线C的极坐标方程为ρ=4cos(θ- ),可化为
),可化为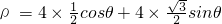 ,
,
∴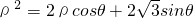 ,
,
∴曲线C的普通方程为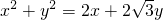 ,
,
即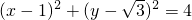 ,
,
∴曲线C是圆心为C ,半径r=2的圆.
,半径r=2的圆.
(Ⅱ)方法一:∵r=2,弦|AB|≥ ,
,
根据圆心C到直线l的距离d=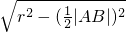 ,
,
∴d≤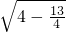 =
= .
.
当 时,圆心C到直线l的距离是1
时,圆心C到直线l的距离是1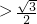 ,不成立;
,不成立;
当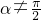 时,设k=tanα,则l:
时,设k=tanα,则l: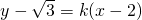 .
.
d=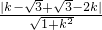 =
=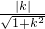
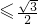 ,
,
解得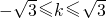 ,即
,即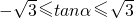 .
.
∵0≤α<π,∴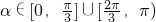 ,即为α的取值范围.
,即为α的取值范围.
方法二:把 代入曲线C的方程
代入曲线C的方程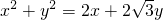 ,
,
化为t2+2tcosα-3=0,
∴t1+t2=-2cosα,t1t2=-3.
∴|AB|=|t1-t2|=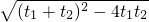 =
=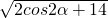 ,
,
∵|AB|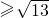 ,
,
∴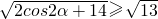 ,
,
∴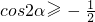 ,
,
∵0≤α<π,∴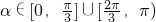 ,即为α的取值α
,即为α的取值α
分析:(Ⅰ)利用公式x=ρcosθ,y=ρsinθ,即可把极坐标方程化为普通方程;
(Ⅱ)方法一:利用圆心C到直线l的距离d、r、 三者之间的关系:d=
三者之间的关系:d=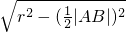 ,及|AB|
,及|AB|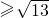 ,即可求出答案;
,即可求出答案;
方法二:把直线的参数方程代入圆的普通方程化为关于t的一元二次方程,利用根与系数的关系及弦长公式|AB|=|t1-t2|和|AB|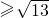 即可得出的答案.
即可得出的答案.
点评:正确利用圆心C到直线l的距离d、r、 三者之间的关系:d=
三者之间的关系:d=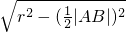 ,及直线l的参数方程中的t的意义是解题的关键.
,及直线l的参数方程中的t的意义是解题的关键.
 ),可化为
),可化为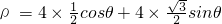 ,
,∴
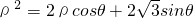 ,
,∴曲线C的普通方程为
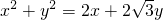 ,
,即
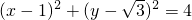 ,
,∴曲线C是圆心为C
 ,半径r=2的圆.
,半径r=2的圆.(Ⅱ)方法一:∵r=2,弦|AB|≥
 ,
,根据圆心C到直线l的距离d=
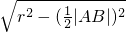 ,
,∴d≤
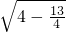 =
= .
.当
 时,圆心C到直线l的距离是1
时,圆心C到直线l的距离是1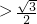 ,不成立;
,不成立;当
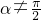 时,设k=tanα,则l:
时,设k=tanα,则l: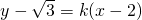 .
.d=
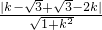 =
=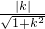
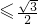 ,
,解得
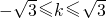 ,即
,即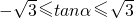 .
.∵0≤α<π,∴
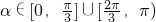 ,即为α的取值范围.
,即为α的取值范围.方法二:把
 代入曲线C的方程
代入曲线C的方程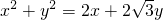 ,
,化为t2+2tcosα-3=0,
∴t1+t2=-2cosα,t1t2=-3.
∴|AB|=|t1-t2|=
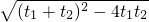 =
=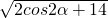 ,
,∵|AB|
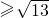 ,
,∴
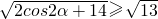 ,
,∴
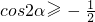 ,
,∵0≤α<π,∴
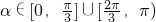 ,即为α的取值α
,即为α的取值α分析:(Ⅰ)利用公式x=ρcosθ,y=ρsinθ,即可把极坐标方程化为普通方程;
(Ⅱ)方法一:利用圆心C到直线l的距离d、r、
 三者之间的关系:d=
三者之间的关系:d=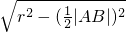 ,及|AB|
,及|AB|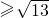 ,即可求出答案;
,即可求出答案;方法二:把直线的参数方程代入圆的普通方程化为关于t的一元二次方程,利用根与系数的关系及弦长公式|AB|=|t1-t2|和|AB|
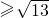 即可得出的答案.
即可得出的答案.点评:正确利用圆心C到直线l的距离d、r、
 三者之间的关系:d=
三者之间的关系:d=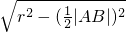 ,及直线l的参数方程中的t的意义是解题的关键.
,及直线l的参数方程中的t的意义是解题的关键. 
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目