题目内容
设A>0,ω>0,0≤?<2π,函数f(x)=Asin(ωx+?),g(x)=Asin(2ωx+?),则函数f(x)在区间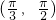 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的
内为增函数的
- A.既不充分也不必要条件
- B.充分不必要条件
- C.必要不充分条件
- D.充分必要条件
D
分析:根据f(x)=Asin(ωx+?)在区间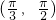 内为增函数,结合A>0,ω>0,0≤?<2π,判断f(x)=Asin(ωx+?)中ω、φ的范围,再根据g(x)=Asin(2ωx+?),在区间
内为增函数,结合A>0,ω>0,0≤?<2π,判断f(x)=Asin(ωx+?)中ω、φ的范围,再根据g(x)=Asin(2ωx+?),在区间 内为增函数,判断g(x)=Asin(2ωx+?),中ω、φ的范围,最后根据充要条件定义得到结论.
内为增函数,判断g(x)=Asin(2ωx+?),中ω、φ的范围,最后根据充要条件定义得到结论.
解答:∵A>0,ω>0,0≤?<2π,
∴当f(x)=Asin(ωx+?)在区间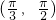 内为增函数时,
内为增函数时,
则
即:
即g(x)=Asin(2ωx+?)在区间 内为增函数
内为增函数
即函数f(x)在区间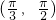 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的充分条件,
内为增函数的充分条件,
反之函数g(x)在区间 内为增函数
内为增函数
即:
则
f(x)=Asin(ωx+?)在区间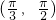 内也为增函数
内也为增函数
即函数f(x)在区间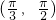 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的必要条件,
内为增函数的必要条件,
故函数f(x)在区间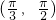 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的充分必要条件
内为增函数的充分必要条件
故选:D
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:根据f(x)=Asin(ωx+?)在区间
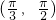 内为增函数,结合A>0,ω>0,0≤?<2π,判断f(x)=Asin(ωx+?)中ω、φ的范围,再根据g(x)=Asin(2ωx+?),在区间
内为增函数,结合A>0,ω>0,0≤?<2π,判断f(x)=Asin(ωx+?)中ω、φ的范围,再根据g(x)=Asin(2ωx+?),在区间 内为增函数,判断g(x)=Asin(2ωx+?),中ω、φ的范围,最后根据充要条件定义得到结论.
内为增函数,判断g(x)=Asin(2ωx+?),中ω、φ的范围,最后根据充要条件定义得到结论.解答:∵A>0,ω>0,0≤?<2π,
∴当f(x)=Asin(ωx+?)在区间
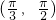 内为增函数时,
内为增函数时,则

即:

即g(x)=Asin(2ωx+?)在区间
 内为增函数
内为增函数即函数f(x)在区间
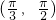 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的充分条件,
内为增函数的充分条件,反之函数g(x)在区间
 内为增函数
内为增函数即:

则

f(x)=Asin(ωx+?)在区间
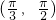 内也为增函数
内也为增函数即函数f(x)在区间
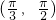 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的必要条件,
内为增函数的必要条件,故函数f(x)在区间
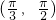 内为增函数是函数g(x)在区间
内为增函数是函数g(x)在区间 内为增函数的充分必要条件
内为增函数的充分必要条件故选:D
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
