题目内容
在数列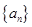 中,已知
中,已知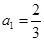 ,
,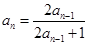 .
.
(1)求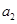 、
、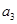 并判断
并判断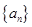 能否为等差或等比数列;
能否为等差或等比数列;
(2)令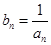 ,求证:
,求证: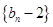 为等比数列;
为等比数列;
(3)求数列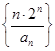 的前n项和
的前n项和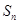 .
.
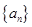 中,已知
中,已知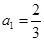 ,
,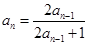 .
.(1)求
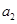 、
、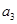 并判断
并判断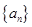 能否为等差或等比数列;
能否为等差或等比数列;(2)令
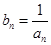 ,求证:
,求证: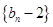 为等比数列;
为等比数列;(3)求数列
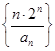 的前n项和
的前n项和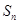 .
.(1) 既不是等差数列也不是等比数列;(2)详见试题解析;(3)
既不是等差数列也不是等比数列;(2)详见试题解析;(3) .
.
 既不是等差数列也不是等比数列;(2)详见试题解析;(3)
既不是等差数列也不是等比数列;(2)详见试题解析;(3) .
.试题分析:(1)分别令
 可得
可得 由等差数列及等比数列定义可得
由等差数列及等比数列定义可得 不是等差数列也不是等比数列;(2)详见试题解析;(3)在(2)的基础上先求
不是等差数列也不是等比数列;(2)详见试题解析;(3)在(2)的基础上先求 ,在求
,在求 得数列
得数列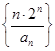 的前
的前 项和
项和 的表达式,最后根据
的表达式,最后根据 的表达式的结构特征利用错位相减法求
的表达式的结构特征利用错位相减法求 .
.试题解析:(1)解:分别令
 得
得 不是等差数列也不是等比数列. 4分
不是等差数列也不是等比数列. 4分(2)
 是等比数列. 8分
是等比数列. 8分(3)由(2)知:
 .
.令
 ,则
,则 ,两式相减得
,两式相减得
 . 13分
. 13分 项和的求法.
项和的求法.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
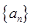 的首项
的首项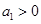 ,公比
,公比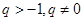 ,设数列
,设数列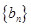 的通项公式
的通项公式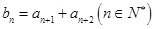 ,数列
,数列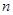 项和分别记为
项和分别记为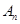 ,
, ,试比较
,试比较 的等比数列前
的等比数列前 项和为15,前
项和为15,前 项和为 .
项和为 . 为等比数列,
为等比数列, 是它的前
是它的前 项和。若
项和。若 ,且
,且 与
与 的等差中项为
的等差中项为 ,则
,则 = .
= .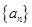 中,
中,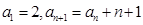 ,则通项
,则通项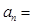 _ .
_ . 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 .若
.若 ,
, ,
, ,则
,则 ______.
______. 满足
满足 ,且
,且 ,则当
,则当 时,
时, ( )
( )


