题目内容
若对任意实数x和正常数t,都有f(x+t)=- 成立,则函数f(x)最小正周期为________.
成立,则函数f(x)最小正周期为________.
2t
分析:利用周期函数的定义f(x+T)=f(x)(T≠0),对于正常数t,f(x+t+t)=- =f(x),可求得函数f(x)最小正周期.
=f(x),可求得函数f(x)最小正周期.
解答:∵ ,∴
,∴ ,
,
∴函数f(x)最小正周期为2t.
故答案为:2t.
点评:本题考查函数的周期性,解题的关键是利用函数周期的定义.
分析:利用周期函数的定义f(x+T)=f(x)(T≠0),对于正常数t,f(x+t+t)=-
 =f(x),可求得函数f(x)最小正周期.
=f(x),可求得函数f(x)最小正周期.解答:∵
 ,∴
,∴ ,
,∴函数f(x)最小正周期为2t.
故答案为:2t.
点评:本题考查函数的周期性,解题的关键是利用函数周期的定义.

练习册系列答案
相关题目
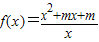 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;