题目内容
由不等式|x-2|+|x+3|>k恒成立,求k的取值范围.
解:已知不等式|x-2|+|x+3|>k恒成立,即需要k小于|x-2|+|x+3|的最小值即可.
故设函数y=|x-2|+|x+3|. 设2、-3、x在数轴上所对应的点分别是A、B、P.
则函数y=|x-2|+|x+3|的含义是P到A的距离与P到B的距离的和.
可以分析到当P在A和B的中间的时候,距离和为线段AB的长度,此时最小.
即:|x-2|+|x+3|=|PA|+|PB|≥|AB|=5.即|x-2|+|x+3|的最小值为5.
即:k≤5.
分析:首先分析题目已知不等式|x-2|+|x+3|>k恒成立,求k的取值范围,即需要k小于|x-2|+|x+3|的最小值即可,对于求
|x-2|+|x+3|的最小值,可以分析它几何意义:在数轴上点x到点2的距离加上点x到点-3的距离.分析得当x在2和-3之间的时候,取最小值,即可得到答案.
点评:此题主要考查不等式恒成立的问题,其中涉及到绝对值不等式求最值的问题,对于y=|x-a|+|x-b|类型的函数可以用分析几何意义的方法求最小值.
故设函数y=|x-2|+|x+3|. 设2、-3、x在数轴上所对应的点分别是A、B、P.
则函数y=|x-2|+|x+3|的含义是P到A的距离与P到B的距离的和.
可以分析到当P在A和B的中间的时候,距离和为线段AB的长度,此时最小.
即:|x-2|+|x+3|=|PA|+|PB|≥|AB|=5.即|x-2|+|x+3|的最小值为5.
即:k≤5.
分析:首先分析题目已知不等式|x-2|+|x+3|>k恒成立,求k的取值范围,即需要k小于|x-2|+|x+3|的最小值即可,对于求
|x-2|+|x+3|的最小值,可以分析它几何意义:在数轴上点x到点2的距离加上点x到点-3的距离.分析得当x在2和-3之间的时候,取最小值,即可得到答案.
点评:此题主要考查不等式恒成立的问题,其中涉及到绝对值不等式求最值的问题,对于y=|x-a|+|x-b|类型的函数可以用分析几何意义的方法求最小值.

练习册系列答案
相关题目
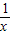 ≥2
≥2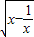 =2,x+
=2,x+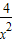 =
=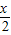 +
+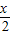 +
+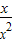 ≥3
≥3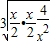 =3,x+
=3,x+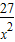 =
=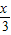 +
+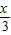 +
+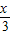 +
+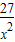 ≥4
≥4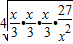 =4,….在x>0条件下,请根据上述不等式归纳出一个一般性的不等式 .
=4,….在x>0条件下,请根据上述不等式归纳出一个一般性的不等式 .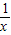 ≥2
≥2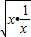 =2,x+
=2,x+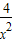 =
=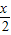 +
+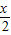 +
+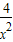 ≥33
≥33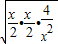 =3…,启发我们可以得出推广结论:x+
=3…,启发我们可以得出推广结论:x+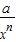 ≥n+1(n∈N+)则a= .
≥n+1(n∈N+)则a= .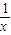 ≥2
≥2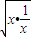 =2,x+
=2,x+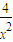 =
=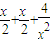 ≥3
≥3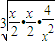 =3,…,可以推出结论:x+
=3,…,可以推出结论:x+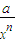 ≥n+1(n∈N*),则a=( )
≥n+1(n∈N*),则a=( )