题目内容
若直线y=2x上存在点(x,y)满足 则实数m的最大值为 ( )
则实数m的最大值为 ( )
| A.-1 | B.1 | C. | D.2 |
B
解析试题分析:由题意得,y=2x,与x+y-3=0确定交点坐标为(1,2)要使直线y=2x上存在点(x,y)满足约束条件
则可知m 1, 由此可得结论.故选B
1, 由此可得结论.故选B
考点:本试题主要考查了线性规划知识的运用,考查学生的理解能力,属于基础题.
点评:解决该试题的关键是对于交点的确定,然后结合图形来确定参数m的范围。

练习册系列答案
相关题目
设变量 满足约束条件:
满足约束条件: ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
设 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
| A.5 | B.7 | C.3 | D.-8 |
表示如图中阴影部分所示平面区域的不等式组是( )
A. | B. |
C. | D. |
已知变量 满足
满足 ,目标函数是
,目标函数是 ,则有( )
,则有( )
A. | B.  无最小值 无最小值 |
C. 无最大值 无最大值 | D. 既无最大值,也无最小值 既无最大值,也无最小值 |
已知点 在不等式组
在不等式组 确定的平面区域内,则点
确定的平面区域内,则点 所在平面区域的面积是( )
所在平面区域的面积是( )
A. | B. | C. | D. |
若实数 满足
满足 则
则 的最大值是
的最大值是
| A.0 | B.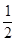 | C. 2 | D.3 |
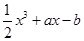 在区间[-1,1]上有且仅有一个零点的概率为
在区间[-1,1]上有且仅有一个零点的概率为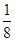

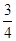
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值是
的最大值是  B.
B. C.
C. D.
D.