题目内容
已知a,b是实数,若直线(b2-2)x+ay+1=0与直线x+ay=0垂直,则a•b的最大值为
1
1
.分析:先由条件得到两直线的斜率都存在,根据斜率之积等于-1结合基本不等式求出对应的结论即可.
解答:解:因为直线(b2-2)x+ay+1=0与直线x+ay=0垂直,
所以两直线的斜率均存在;
所以-
•(-
)=-1⇒(b2-2)+a2=0,
即a2+b2=2≥2ab
∴ab≤1
故答案为:1.
所以两直线的斜率均存在;
所以-
| b2-2 |
| a |
| 1 |
| a |
即a2+b2=2≥2ab
∴ab≤1
故答案为:1.
点评:本题考查两条直线垂直的判定,考查计算推理能力,是基础题.

练习册系列答案
相关题目
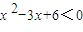 成立;
成立;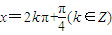 是tanx=1的充要条件.
是tanx=1的充要条件.