题目内容
下列命题中正确的命题个数为( )①存在一个实数x使不等式
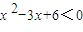 成立;
成立;②已知a,b是实数,若ab=0,则a=0且b=0;
③
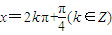 是tanx=1的充要条件.
是tanx=1的充要条件.A.0
B.1
C.2
D.3
【答案】分析:对于①,由于 的△<0,从而
的△<0,从而 恒成立,据此对①进行判断;②若ab=0,则a=0或b=0;从而进行判断;③当
恒成立,据此对①进行判断;②若ab=0,则a=0或b=0;从而进行判断;③当 时,得出 tan(2kπ+
时,得出 tan(2kπ+ )=tan
)=tan  =1,“x=2kπ+
=1,“x=2kπ+ (k∈Z)”是“tanx=1”成立的充分条件;举反例x=
(k∈Z)”是“tanx=1”成立的充分条件;举反例x= 时,tan
时,tan  =1.推出“x=2kπ+
=1.推出“x=2kπ+ (k∈Z)”是“tanx=1”成立的不必要条件,据此进行判断.
(k∈Z)”是“tanx=1”成立的不必要条件,据此进行判断.
解答:解: 的△=9-26<0,∴
的△=9-26<0,∴ 恒成立,
恒成立,
故①不正确;
对于②若ab=0,则a=0或b=0,故②不正确;
③tan(2kπ+ )=tan
)=tan  =1,所以充分;但反之不成立,如 tan
=1,所以充分;但反之不成立,如 tan  =1.
=1.
故 是tanx=1的充分不必要条件.故③不正确.
是tanx=1的充分不必要条件.故③不正确.
∴命题中正确的命题个数为0.
故选A.
点评:本题主要考查了命题的真假判断与应用,必要条件、充分条件与充要条件的判断.充分条件与必要条件是中学数学最重要的数学概念之一,要理解好其中的概念.
 的△<0,从而
的△<0,从而 恒成立,据此对①进行判断;②若ab=0,则a=0或b=0;从而进行判断;③当
恒成立,据此对①进行判断;②若ab=0,则a=0或b=0;从而进行判断;③当 时,得出 tan(2kπ+
时,得出 tan(2kπ+ )=tan
)=tan  =1,“x=2kπ+
=1,“x=2kπ+ (k∈Z)”是“tanx=1”成立的充分条件;举反例x=
(k∈Z)”是“tanx=1”成立的充分条件;举反例x= 时,tan
时,tan  =1.推出“x=2kπ+
=1.推出“x=2kπ+ (k∈Z)”是“tanx=1”成立的不必要条件,据此进行判断.
(k∈Z)”是“tanx=1”成立的不必要条件,据此进行判断.解答:解:
 的△=9-26<0,∴
的△=9-26<0,∴ 恒成立,
恒成立,故①不正确;
对于②若ab=0,则a=0或b=0,故②不正确;
③tan(2kπ+
 )=tan
)=tan  =1,所以充分;但反之不成立,如 tan
=1,所以充分;但反之不成立,如 tan  =1.
=1.故
 是tanx=1的充分不必要条件.故③不正确.
是tanx=1的充分不必要条件.故③不正确.∴命题中正确的命题个数为0.
故选A.
点评:本题主要考查了命题的真假判断与应用,必要条件、充分条件与充要条件的判断.充分条件与必要条件是中学数学最重要的数学概念之一,要理解好其中的概念.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 所成的角相等,那么a∥b
所成的角相等,那么a∥b