题目内容
已知函数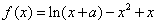 ,
,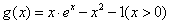 ,且
,且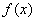 点
点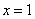 处取得极值.
处取得极值.
(Ⅰ)求实数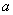 的值;
的值;
(Ⅱ)若关于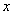 的方程
的方程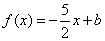 在区间
在区间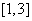 上有解,求
上有解,求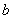 的取值范围;
的取值范围;
(Ⅲ)证明: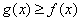 .
.
【答案】(1) ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.
试题解析:(Ⅰ)∵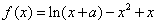 ,∴
,∴
∵函数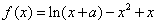 在点
在点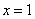 处取得极值,
处取得极值,
∴ ,即当
,即当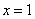 时
时 ,
,
∴ ,则得
,则得 .经检验符合题意
.经检验符合题意
(Ⅱ)∵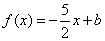 ,∴
,∴ ,
,
∴ .
.
令 ,
,
则 .
.
∴当 时,
时, 随
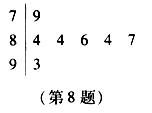
随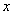 的变化情况表:
的变化情况表:
|
| 1 | (1,2) | 2 | (2,3) | 3 |
|
| + | 0 | - | ||
|
| ↗ | 极大值 | ↘ |
计算得: ,
, ,
, ,
,
所以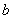 的取值范围为
的取值范围为 。
。
(Ⅲ)证明:令

 ,
,
则
 ,
,
令 ,则
,则 ,
,
 函数
函数 在
在 递增,
递增, 在
在 上的零点最多一个
上的零点最多一个
又
 ,
, ,
,
 存在唯一的
存在唯一的 使得
使得 ,
,
且当 时,
时, ;当
;当 时,
时, .
.
即当 时,
时, ;当
;当 时,
时, .
.

 在
在 递减,在
递减,在 递增,
递增,
从而
 .
.
由 得
得 即
即 ,两边取对数得:
,两边取对数得: ,
,
 ,
,

 ,
,
从而证得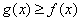 .
.

练习册系列答案
相关题目



 ,且当
,且当 ∈[-3,-2]时,
∈[-3,-2]时, ,则
,则 的值是____________.
的值是____________.
 对定义域
对定义域
 内的任意
内的任意
 都有
都有
 ,且当
,且当
 时,其导数
时,其导数
 满足
满足
 ,若
,若
 ,则 ( )
,则 ( )
 B.
B.



 ,其导函数为
,其导函数为
 处的切线
处的切线
 的方程;
的方程;
 +…+
+…+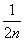 >
>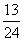 (n≥2,n∈N*)的过程中,由n=k递推到n=k+1时,不等式的左边( )
(n≥2,n∈N*)的过程中,由n=k递推到n=k+1时,不等式的左边( )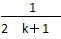 B.增加了一项
B.增加了一项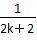 ,并减少了
,并减少了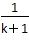
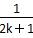 和
和 ,BC=3,过点C作圆O的切线
,BC=3,过点C作圆O的切线 ,过点A作
,过点A作
 是等差数列,且
是等差数列,且 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则