题目内容
已知f（x）=2sin（x+
）（x∈R）．（Ⅰ）求函数f（x）的周期和最大值；
（Ⅱ）若f（A-
）=
，求cos2A的值．
【答案】分析：（Ⅰ）由函数f（x）=2sin（x+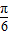
），可得它的周期，以及函数f （x）的最大值．
（Ⅱ）由 f（A-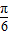
）=2sinA=
，求得sinA的值，再由cos2A=1-2sin2A，运算求得结果．
解答：解：（Ⅰ）∵f（x）=2sin（x+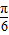
），故函数的周期为T=2π，
当x+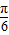
=2kπ+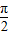
，即x=2kπ+
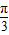，（k∈Z）时，f （x）取得最大值为2．…（6分）
（Ⅱ）∵f（A-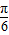
）=2sinA=
，∴sinA=
．…（9分）
∴cos2A=1-2sin2A=
．…（12分）
点评：本题主要考查三角函数的周期性和最值，二倍角的余弦公式的应用，属于中档题．
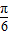），可得它的周期，以及函数f （x）的最大值． （Ⅱ）由 f（A-
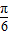）=2sinA=，求得sinA的值，再由cos2A=1-2sin2A，运算求得结果．解答：解：（Ⅰ）∵f（x）=2sin（x+
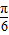），故函数的周期为T=2π，当x+
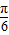=2kπ+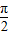，即x=2kπ+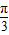，（k∈Z）时，f （x）取得最大值为2．…（6分）（Ⅱ）∵f（A-
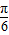）=2sinA=，∴sinA=．…（9分）∴cos2A=1-2sin2A=
．…（12分）点评：本题主要考查三角函数的周期性和最值，二倍角的余弦公式的应用，属于中档题．
练习册系列答案
相关题目
（2011•孝感模拟）已知f（x）=2sin（ωx+φ）的部分图象如图所示，则f（x）的表达式为（ ）