题目内容
“m＜1”是“函数f（x）=x2+x+m有零点”的（ ）A．充分非必要条件
B．充要条件
C．必要非充分条件
D．既不充分也不必要条件
【答案】分析：f（x）=x2+x+m有零点?△=1-4m≥0即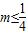
，然后根据条件即可判断
解答：解：∵f（x）=x2+x+m有零点
∴△=1-4m≥0即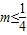
当m＜1时，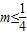
不一定成立；但是当
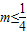时，m＜1一定成立
故m＜1”是“函数f（x）=x2+x+m有零点”的必要不充分条件
故选C
点评：本题主要考查了充分条件与必要条件的判断，解题 的关键是寻求函数f（x）=x2+x+m有零点的等价条件
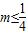，然后根据条件即可判断解答：解：∵f（x）=x2+x+m有零点
∴△=1-4m≥0即
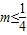
当m＜1时，
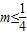不一定成立；但是当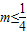时，m＜1一定成立故m＜1”是“函数f（x）=x2+x+m有零点”的必要不充分条件
故选C
点评：本题主要考查了充分条件与必要条件的判断，解题 的关键是寻求函数f（x）=x2+x+m有零点的等价条件
练习册系列答案
相关题目