Question

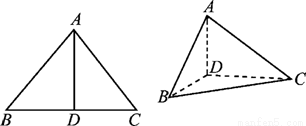
如图,在△ABC中,∠ABC＝45°,∠BAC＝90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC＝90°.  (1)证明：平面ADB⊥平面BDC； (2)若BD＝1,求三棱锥D－ABC的表面积.

 

 

 

 

 

 

Answer 1

【答案】

 

 (1)∵折起前AD是BC边上的高,∴当△ABD折起后,AD⊥DC,AD⊥DB.

又DB∩DC＝D.∴AD⊥平面BDC.

∵AD⊥平面ABD,  ∴平面ABD⊥平面BDC.

(2)由(1)知,DA⊥DB,DB⊥DC,DC⊥DA, DB＝DA＝DC＝1.

∴AB＝BC＝CA＝. 从而S△DAB＝S△DBC＝S△DCA＝×1×1＝.

S△ABC＝×××sin60°＝.  ∴表面积S＝×3＋＝.

 

【解析】略