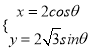题目内容
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】(1)由题意,下潜用时![]() (单位时间),用氧量为
(单位时间),用氧量为![]() (升),
(升),
水底作业时的用氧量为![]() (升), 返回水面用时
(升), 返回水面用时 (单位时间),用氧量为
(单位时间),用氧量为![]() (升),
(升),
∴![]() .
.
(2)![]() ,令
,令![]() 得
得![]() ,
,
在![]() 时,
时,![]() ,函数单调递减,在
,函数单调递减,在![]() 时,
时,![]() ,函数单调递增,
,函数单调递增,
∴当![]() 时,函数在
时,函数在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() 时总用氧量最少,
时总用氧量最少,
当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,
∴![]() 时,总用氧量最少.
时,总用氧量最少.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.