题目内容
已知正实数x,y,设a=x+y,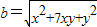 .
.(1)当y=1时,求
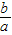 的取值范围;
的取值范围;(2)若以a,b为三角形的两边,第三条边长为c构成三角形,求
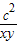 的取值范围.
的取值范围.
【答案】分析:(1)法一:当y=1时,x=a-1,由x,y均为正实数,代入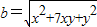 ,可得
,可得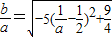 ,进而根据二次函数的图象和性质得到
,进而根据二次函数的图象和性质得到 的取值范围;
的取值范围;
法二:当y=1时,根据a=x+y,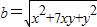 ,可将
,可将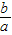 化为
化为 的形式,进而利用基本不等式求出
的形式,进而利用基本不等式求出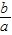 的取值范围;
的取值范围;
(2) ,则
,则 ,由于a,b,c为三角形的三边,由“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组,进而根据对勾函数的单调性,求出
,由于a,b,c为三角形的三边,由“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组,进而根据对勾函数的单调性,求出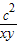 的取值范围.
的取值范围.
解答:解:(1)由题设知,x=a-1,且a=x+1>1
所以,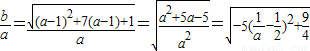
又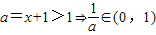
结合二次函数的图象知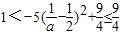
故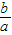 的取值范围为
的取值范围为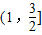
另解:
= ,∵
,∵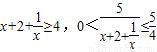 ∴
∴ ,得
,得 的取值范围为
的取值范围为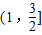
(2)设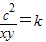 ,则
,则
∵ 恒成立,
恒成立,
即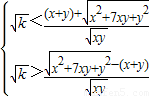
 ,恒成立
,恒成立
令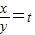 ,由于
,由于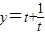 在[1,+∞)是增函数,令
在[1,+∞)是增函数,令 ,则
,则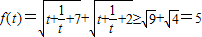
又∵ ∴
∴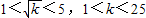 ,
,
得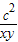 的取值范围为(1,25)
的取值范围为(1,25)
点评:本题考查的知识点是函数的值域,基本不等式在求函数最值时的应用,对勾函数的单调性,其中(1)的关键是将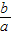 的表达式,根据已知进行变形,为二次函数性质的应用或基本不等式的应用创造条件,(2)的关键是设
的表达式,根据已知进行变形,为二次函数性质的应用或基本不等式的应用创造条件,(2)的关键是设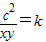 ,并根据三角形的三边“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组.
,并根据三角形的三边“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组.
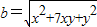 ,可得
,可得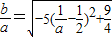 ,进而根据二次函数的图象和性质得到
,进而根据二次函数的图象和性质得到 的取值范围;
的取值范围;法二:当y=1时,根据a=x+y,
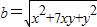 ,可将
,可将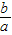 化为
化为 的形式,进而利用基本不等式求出
的形式,进而利用基本不等式求出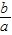 的取值范围;
的取值范围;(2)
 ,则
,则 ,由于a,b,c为三角形的三边,由“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组,进而根据对勾函数的单调性,求出
,由于a,b,c为三角形的三边,由“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组,进而根据对勾函数的单调性,求出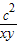 的取值范围.
的取值范围.解答:解:(1)由题设知,x=a-1,且a=x+1>1
所以,
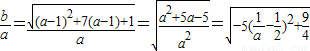
又
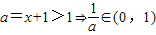
结合二次函数的图象知
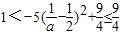
故
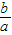 的取值范围为
的取值范围为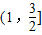
另解:

=
 ,∵
,∵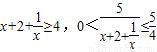 ∴
∴ ,得
,得 的取值范围为
的取值范围为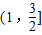
(2)设
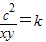 ,则
,则
∵
 恒成立,
恒成立,即
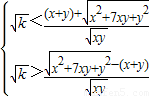
 ,恒成立
,恒成立令
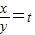 ,由于
,由于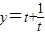 在[1,+∞)是增函数,令
在[1,+∞)是增函数,令 ,则
,则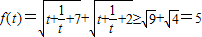
又∵
 ∴
∴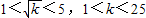 ,
,得
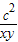 的取值范围为(1,25)
的取值范围为(1,25)点评:本题考查的知识点是函数的值域,基本不等式在求函数最值时的应用,对勾函数的单调性,其中(1)的关键是将
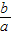 的表达式,根据已知进行变形,为二次函数性质的应用或基本不等式的应用创造条件,(2)的关键是设
的表达式,根据已知进行变形,为二次函数性质的应用或基本不等式的应用创造条件,(2)的关键是设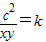 ,并根据三角形的三边“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组.
,并根据三角形的三边“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组. 
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目